中国城市数字经济对物流业高质量发展的影响

      数学学科独有的形式化抽象特征，如精深的数学概念、烦琐的演算过程、复杂的数形关系和多变的几何位置关系等，往往由于教与学手段的限制而令人“望而却步”.运用学科软件进行数学教学，能改变“重形式定义，轻意象表征”的教学模式.数学教学从整合走向融合，需要建立图形图像、符号表达与数值处理间的多元表征联系，需要严谨、精确和形式化的数学活动过程描述，需要构建与数学研究相适应的、丰富的探索性认知环境[1].

      三视图是学生学习立体几何的基础，也是学生建立空间观念的开始.学生从初中开始接触三视图，到了高中阶段加以学习，其对于三视图已有一定的认识，但由于空间想象力不足，根据三视图还原几何体成为学生学习的难点.

      一、问题的提出

      （2014·全国Ⅰ卷，理12）如图1，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（

       ）.

      

      

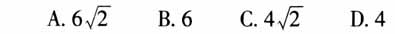
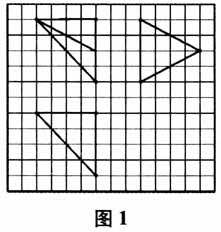      这道题目是2014年高考理科数学全国Ⅰ卷选择题的第12题，难度不低.笔者在一次测试中发现，所教的高三年级其中一个班66人中只有7人做对，这一结果让笔者感到非常震惊，于是找了一些学生进行访谈，发现学生由于空间想象力不足，无法还原出原来的几何体.在实际教学中，笔者发现很多教师在讲授这部分知识的时候通常感到“力不从心”.因此，笔者对此进行了专题研究，结合信息技术的优势，利用玲珑画板的3D和“任意切割”功能，根据三视图的特点，总结出用“三维切割法”还原三视图.

      二、实验过程

      1.实验前测

      笔者充分利用课堂派软件互动性功能进行了实验前测.课前呈现2014年高考理科数学全国Ⅰ卷选择题第12题，并给学生3分钟时间独立完成，然后利用手机进入课堂派平台进行提交.教师在课堂派平台上进行统计发现，35人的实验样本中只有3人答对，说明学生对该题的解题能力尚有欠缺.由此，笔者设置本节课的问题情境：三视图如何还原几何体？

      2.教学过程

      根据三视图的定义，三视图的形成主要是由三束不同方向的光照射形成的.笔者制作了如下页图2～图4的动画图形，展示三视图的形成过程.通过展示，学生不仅理解了三视图，而且也理解了为什么三视图是这样排列的.与此同时也带给我们解决问题的灵感：三个维度的面围成一个长方体（或者正方体），是不是就可以以一个长方体（或者正方体）作为“基础几何体”，把“三个方向照射”类比为“三个方向切割”，即“三维切割法”还原三视图.

      

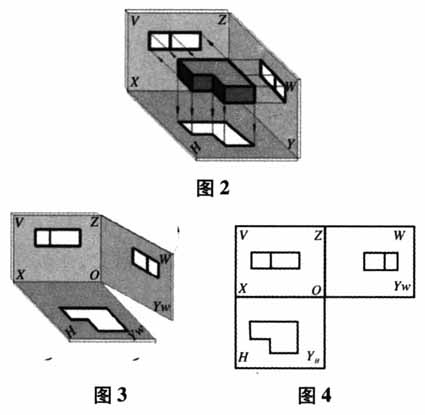      研究发现，既然三视图的形成主要是由三束不同方向的光照射形成的，要得到满足条件的几何体，必须是正视图、侧视图、俯视图全部满足才可以，下文以问题1为例进行说明.

      问题1：如图5，是某几何体的三视图，该几何体直观图的最大面是什么形状？

      

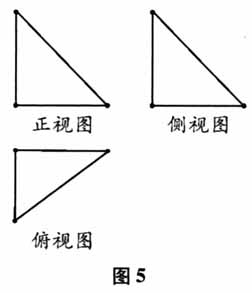      步骤一：构造基础几何体（如图6），然后利用玲珑画板按照图7的位置进行切割（正面切割），得到几何体（如图8-a）.此时，可以使用系统的“三视图”功能进行验证，发现其中的正视图和原来的吻合（如图8-b）.

      

      

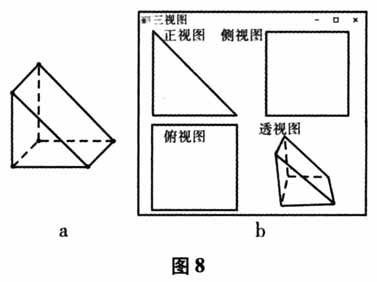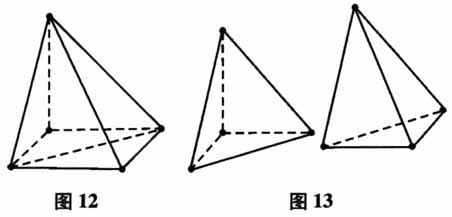
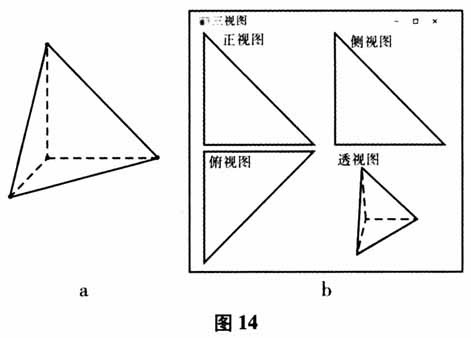
      步骤二：在步骤一得到的几何体（如图9）基础上，再按照图10的位置进行切割（侧面切割），得到几何体（如图11-a）.此时，可以使用系统的“三视图”功能进行验证，发现其中的正视图与侧视图和原来的都吻合（如图11-b）.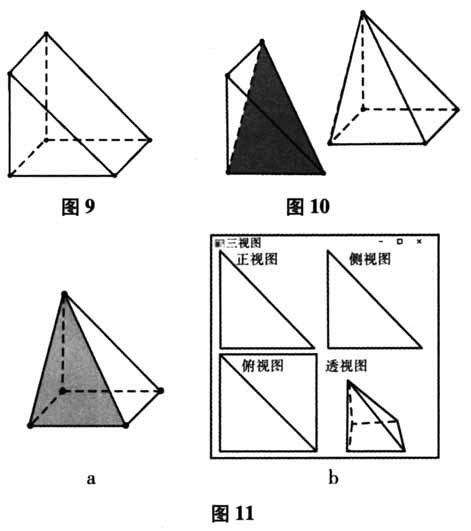

      

      步骤三：在步骤二得到的几何体（如图12）基础上，再按照图13的位置进行切割（俯面切割），得到几何体（如下页图14-a）.此时，可以使用系统的“三视图”功能进行验证，发现其中的正视图、侧视图、俯视图和原来的全部吻合（如下页图14-b）.由此可知，所探求的几何体就是图14-b中的透视图，从而轻松解决三视图还原几何体的问题.