生鲜产品是指经过必要保鲜和简单整理后上架出售的初级产品及现场加工类商品,如水产品、果蔬、肉禽、现烤面包等。[1][2]作为生活必需品,生鲜产品与我们的生活密切相关,相关数据显示,居民平均每周购买生鲜产品约为4.8次,[3]总体市场规模约2万亿左右。[4]文献研究显示,随着经济发展,消费者越来越偏好生鲜产品的新鲜度和服务需求。[5]实践中,元祖与新西兰樱桃直采果园合作,提供源头预冷、全程保鲜、终端冷藏配送等保鲜服务;果琳与本地水果基地合作,提供预冷套袋、冷藏陈列、分切打包等保鲜和货架服务。然而,保鲜投入及货架服务需要权衡诸多成本和收益,成本控制使许多企业保鲜投入不足,生鲜产品损耗严重。 生鲜产品损耗已成为企业及其供应链亟须解决的问题。生鲜产品的流通中,近三成的生鲜产品损耗在供应链各流通环节,损耗额高达千亿元以上,[6]高损耗限制了生鲜供应链发展和企业经营。同时,消费者偏好更加新鲜的产品给供应链的全程保鲜带来了挑战。因此,降低生鲜损耗,有效维持生鲜质量,成为生鲜产品供应链中各参与企业的首要解决问题。近年来,行业环境改善和国家政策支持为解决生鲜产品损耗问题带来了希望。一方面,作为支撑生鲜供应链的关键环节,我国冷链物流行业的市场规模逐年扩大;[4]另一方面,中央和政府十分重视生鲜产品供应链的全程保鲜,近三年的中央一号文件均明确要求加强冷链物流体系建设,为我国冷链物流行业发展创造了利好的政策环境。 合理的货架服务是生鲜企业面临的另一现实考验。近年来,随着生鲜行业竞争日渐激烈,消费者服务需求和企业服务意识日渐提高,将消费体验融入生鲜产品销售的现象逐渐增加,企业欲借助细致的货架服务进一步扩大市场需求。如永辉超市在“超级物种”业务中,提供生鲜产品体验馆,为消费者提供清洗、加工、包装、烹饪等各项货架服务,这些服务在增强体验感的同时,也拉动了体验者(尤其是都市白领)的消费需求。我国城乡居民消费应从量的满足转为质的提升、从有形物质转向更多服务消费(国办发[2017]29号)[7],这表明在国家战略指导和消费者需求转变的形势下,生鲜产品供应链转变竞争方式,在终端销售阶段投入货架服务吸引消费者已成趋势,但货架服务进一步加大了企业的成本投入。 在生鲜产品供应链中,合理定价是企业平衡成本和收益的重要手段。生鲜产品零售商销售的常见产品大多跟随市场定价(即价格外生),而一些特殊生鲜产品,如海鲜、进口水果等,由于其产量少且仅有部分生鲜企业售卖,企业可以自主合理制定价格(即价格内生)。如元祖自主制定所售进口水果的价格,以平衡高昂的保鲜服务成本;而果琳的本地水果价格与市场价一致。鉴于此,生鲜产品的市场定价也是生鲜企业关注的焦点。 为了进一步了解生鲜产品供应链的优化决策及其协调机制,本文从以下两方面展开研究:首先,本文从生鲜产品的易逝率刻画方法、生鲜产品供应链的优化决策模型、协调契约设计三方面综述近年来的相关研究成果;其次,在总结研究成果的基础上探讨进一步可拓展的研究方向。 二、易逝率的刻画方法 易逝性是生鲜产品的一个重要属性,保鲜技术投入能控制生鲜产品的衰减速度。在Wagner & Whiting[8]将变质率刻画进流行产品的库存模型之后,Moon[9]、Hsu[10]、魏广明[11]等学者相继建立生鲜产品衰减控制模型,包括常数变质率、时变变质率和可控变质率。 在生鲜产品供应链库存管理的早期研究中,学者们采用常数刻画产品变质率。兰洪杰等[12]基于常数变质率研究供应商和零售商的协调补货策略;Hsieh & Dye[13]研究基于常数变质率的零售商补货策略和定价决策,类似的研究还有段永瑞[14],陈杰等[15]。由于常数变质率在应用中有较大局限性,所以本文主要梳理时变变质率和可控变质率。 (一)时变变质率 生鲜产品的变质程度与流通时间相关,称为时变变质率,分为线性时变变质率和非线性时变变质率。苏兵等[16]用乘法形式(θ×T)表示生鲜产品的变质情况,Sarkar et al.[17]利用二次多项式刻画变质率,上述研究假定变质率与时间的关系固定。另一些学者指出在空气湿度、温度等环境因素影响下,生鲜产品的变质率与时间关系难以确定,如李贵萍等[18]运用函数形式未知的θ(t)刻画时变变质率。因此,引入了生存函数表示生鲜产品保质期大于其流通时长的概率,成为新的研究路径。 Covert et al.[19]为了表明产品变质率会随时间增加而增加,首先提出两参数的Weibull分布变质函数,表述为

,y(t)和r(t)为变质时间的概率密度和累积分布函数,γ和δ分别表示储存规模因子和环境因子。之后,许多学者在不同的决策背景下运用了两参数的Weibull分布函数,如黄卫来和黄松[20]、段永瑞和李贵萍[21]等。 两参数Weibull函数的假设意味着产品从入库伊始便开始变质,为了更贴近现实情况,Shah[22]首先将保鲜期因子考虑进Weibull函数,刻画了三参数的Weibull分布变质函数,表达式变为
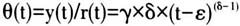
。之后,王宪杰[23]、Yang[24]和王淑云[25]等分别在零售商库存管理模型和一体化库存中对三参数的Weibull分布变质率进行了研究。
 ,y(t)和r(t)为变质时间的概率密度和累积分布函数,γ和δ分别表示储存规模因子和环境因子。之后,许多学者在不同的决策背景下运用了两参数的Weibull分布函数,如黄卫来和黄松[20]、段永瑞和李贵萍[21]等。 两参数Weibull函数的假设意味着产品从入库伊始便开始变质,为了更贴近现实情况,Shah[22]首先将保鲜期因子考虑进Weibull函数,刻画了三参数的Weibull分布变质函数,表达式变为
,y(t)和r(t)为变质时间的概率密度和累积分布函数,γ和δ分别表示储存规模因子和环境因子。之后,许多学者在不同的决策背景下运用了两参数的Weibull分布函数,如黄卫来和黄松[20]、段永瑞和李贵萍[21]等。 两参数Weibull函数的假设意味着产品从入库伊始便开始变质,为了更贴近现实情况,Shah[22]首先将保鲜期因子考虑进Weibull函数,刻画了三参数的Weibull分布变质函数,表达式变为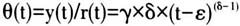 。之后,王宪杰[23]、Yang[24]和王淑云[25]等分别在零售商库存管理模型和一体化库存中对三参数的Weibull分布变质率进行了研究。
。之后,王宪杰[23]、Yang[24]和王淑云[25]等分别在零售商库存管理模型和一体化库存中对三参数的Weibull分布变质率进行了研究。