普通高中数学课程标准提出了六大学科核心素养,包括数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.“数学在本质上研究的是抽象的东西,数学的发展所依赖的最重要的基本思想也就是抽象”,数学抽象也是形成理性思维的重要基础,反映了数学的本质特征,贯穿在数学产生、发展、应用的过程中.课程标准希望学生通过高中数学课程的学习,能在情境中抽象出数学概念、命题、方法和体系,积累从具体到抽象的活动经验. 史宁中教授认为数学抽象有两个层次:从辨别到概括为第一次抽象,表现为用自然语言表达的直观描述;概括后到形式化,完成符号表达为第二次抽象.函数作为高中数学课程内容的主线,主要围绕理解一般的函数概念、学会研究函数的性质、掌握一批具体函数模型、了解函数应用问题、学会运用函数解决这些问题等主题展开.苏教版必修一第二章函数主要关注理解一般的函数概念和学会研究函数的性质两个方面.在初中阶段,学生已经接触过函数,通过观察图象,使用自然语言描述性质,如“随着变量的增大而增大”“函数图象关于轴对称”等等.高中阶段函数则在此基础上完成第二层次抽象,使用更“精致”的代数化、符号化语言进行刻画,引入单调性、奇偶性等概念,对学生数学抽象能力提出了更高的要求,也进一步培养学生数学抽象素养. 章建跃教授在《树立课程意识,落实核心素养》中强调:“众所周知,概念教学是数学教学的重中之重,而得出概念的过程是最典型的数学抽象的过程”.李邦河院士同样认为“数学根本上是玩概念的,不是玩技巧.技巧不足道也!”所以概念教学作为教师培养学生数学抽象素养的重要载体,具有极其重要的作用.而必修一第二章函数中函数定义、单调性、最值和奇偶性均涉及概念教学,并且是高中数学学习的第一个难点,值得重视. 但是目前在函数方面的概念教学存在严重问题,许多教师采用直接给出学生概念,再通过若干个辨析来巩固概念的方法进行教学,看似教学效率极高,但是学生对概念如何从实例中抽象得到没有深刻体会,导致学生对概念的理解不深,数学抽象能力更是没有得到一丝一毫的锻炼和提高,这样的做法是与课程标准的要求背道而驰的.笔者希望结合若干函数教学片段,谈谈在概念教学中如何落实数学抽象素养的培养. 一、教学片段研究 (一)根据已有知识,选择合适例子强调数学概念形成教学 案例1:函数概念教学片段 问题1:我们如何研究函数?研究函数的哪些方面呢? 问题2:在初中已经接触了函数,请大家回忆一下初中函数的定义.然后说说已经学过了哪些具体的函数,并且它们为什么是函数呢? 设计意图:引导学生回忆初中函数的概念,初中使用“变量说”,是函数概念的第一次抽象,具有一定的直观性.突出“两个变量x,y”,对于变量x的“每一个”值,变量y都有“唯一”确定的值与它相对应.引导学生指出对应关系是什么,为抽象符号f的引入做准备,并指出x和y的取值范围,为抽象成两个数集做准备.研究数学对象,一般是建立在已有认识的基础上,这样的切入方式显得并不突兀. 问题3:刚刚说的函数都是解析式形式的,还有其他形式的吗?表格中是1949-1999我国人口数据表(表略),这是一个函数吗?并且说说理由. (学生回答后追问)年份可以取到哪些值呢?人口数呢?它们之间的对应关系是什么? 问题4:一物体从静止开始下落,下落的距离y(单位:m)与下落时间x(单位:s)之间近似地满足关系式
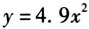
.它是一个函数吗?下落时间和下落距离分别可以取到哪些值呢?它们之间有什么关系吗? 问题5:这是某市一天24小时内的气温变化图,它能构成一个函数吗?时间和温度分别是什么样的数集,它们之间的对应关系是什么?每一个时间都对应唯一的温度吗?
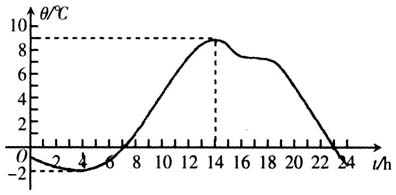
(学生回答后追问)刚刚时间作为自变量,温度作为因变量,那么温度可以作为自变量吗? 问题6:上面的三个例子大家能发现有什么共同特点呢? 设计意图:概念抽象需要典型丰富的例子,通过学生回答问题和追问,可以观察他们对函数概念中“对应法则f”“每一个元素x”“唯一的元素y”“对应”关键词的领悟,形成对函数概念的初步认识,为进一步抽象概括做准备. 问题7:前面我们学习了“集合”,你能用“集合”和对应的语言描述函数的概念吗? 设计意图:通过前面三个案例关于“集合”语言的渗透以及关键字的强调,要求学生从具体的函数中抽象出函数的一般概念,培养学生的数学抽象素养. 到此虽然函数概念教学并未全部完成,但是函数概念的形成已有大致的思路,教学难点在于对抽象符号“f:A→B,y=f(x),x∈A,f(x)∈B”的理解.教师在学生已有认知的基础上,充分利用初中学过的函数和生活实例,让学生领悟对应法则f的含义,体会限定变量x,y的变化范围的必要性,体会在其变化范围内变量的依赖关系.三个合适的例子在本次教学中尤为重要,图象、解析式、表格形式多样,并且学生均可以在短时间内就体会其变量x,y的变化范围以及两者之间的关系.为了认识抽象符号f(x),采用大量的、形式多样的例子为依托,从具体到抽象、从特殊到一般,使学生更好地体会函数概念中所包含的重要信息.
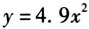 .它是一个函数吗?下落时间和下落距离分别可以取到哪些值呢?它们之间有什么关系吗? 问题5:这是某市一天24小时内的气温变化图,它能构成一个函数吗?时间和温度分别是什么样的数集,它们之间的对应关系是什么?每一个时间都对应唯一的温度吗?
.它是一个函数吗?下落时间和下落距离分别可以取到哪些值呢?它们之间有什么关系吗? 问题5:这是某市一天24小时内的气温变化图,它能构成一个函数吗?时间和温度分别是什么样的数集,它们之间的对应关系是什么?每一个时间都对应唯一的温度吗?  (学生回答后追问)刚刚时间作为自变量,温度作为因变量,那么温度可以作为自变量吗? 问题6:上面的三个例子大家能发现有什么共同特点呢? 设计意图:概念抽象需要典型丰富的例子,通过学生回答问题和追问,可以观察他们对函数概念中“对应法则f”“每一个元素x”“唯一的元素y”“对应”关键词的领悟,形成对函数概念的初步认识,为进一步抽象概括做准备. 问题7:前面我们学习了“集合”,你能用“集合”和对应的语言描述函数的概念吗? 设计意图:通过前面三个案例关于“集合”语言的渗透以及关键字的强调,要求学生从具体的函数中抽象出函数的一般概念,培养学生的数学抽象素养. 到此虽然函数概念教学并未全部完成,但是函数概念的形成已有大致的思路,教学难点在于对抽象符号“f:A→B,y=f(x),x∈A,f(x)∈B”的理解.教师在学生已有认知的基础上,充分利用初中学过的函数和生活实例,让学生领悟对应法则f的含义,体会限定变量x,y的变化范围的必要性,体会在其变化范围内变量的依赖关系.三个合适的例子在本次教学中尤为重要,图象、解析式、表格形式多样,并且学生均可以在短时间内就体会其变量x,y的变化范围以及两者之间的关系.为了认识抽象符号f(x),采用大量的、形式多样的例子为依托,从具体到抽象、从特殊到一般,使学生更好地体会函数概念中所包含的重要信息.
(学生回答后追问)刚刚时间作为自变量,温度作为因变量,那么温度可以作为自变量吗? 问题6:上面的三个例子大家能发现有什么共同特点呢? 设计意图:概念抽象需要典型丰富的例子,通过学生回答问题和追问,可以观察他们对函数概念中“对应法则f”“每一个元素x”“唯一的元素y”“对应”关键词的领悟,形成对函数概念的初步认识,为进一步抽象概括做准备. 问题7:前面我们学习了“集合”,你能用“集合”和对应的语言描述函数的概念吗? 设计意图:通过前面三个案例关于“集合”语言的渗透以及关键字的强调,要求学生从具体的函数中抽象出函数的一般概念,培养学生的数学抽象素养. 到此虽然函数概念教学并未全部完成,但是函数概念的形成已有大致的思路,教学难点在于对抽象符号“f:A→B,y=f(x),x∈A,f(x)∈B”的理解.教师在学生已有认知的基础上,充分利用初中学过的函数和生活实例,让学生领悟对应法则f的含义,体会限定变量x,y的变化范围的必要性,体会在其变化范围内变量的依赖关系.三个合适的例子在本次教学中尤为重要,图象、解析式、表格形式多样,并且学生均可以在短时间内就体会其变量x,y的变化范围以及两者之间的关系.为了认识抽象符号f(x),采用大量的、形式多样的例子为依托,从具体到抽象、从特殊到一般,使学生更好地体会函数概念中所包含的重要信息.