一、引言及文献回顾 目前,对于中国实体经济发展而言,物流业是具有基础性、衔接性和战略性意义的产业。改革开放40年的物流业高级化发展历程表明,物流业转型升级、效率提升先是通过资源集成、功能集成,再是通过两业联动、产业联动实现的(董千里,2018a),具体过程是:由集成体主导物流链、供应链的微观网链与交通运输基础设施的宏观网络对接,再通过集聚、中转、始发,最终到达可以拓展枢纽(节点)城市产业的辐射范围,从而提高物流主通道的时间周转量。物流基础设施建设可加速物流枢纽网络布局形成,衔接并支持微观网链运作与拓展(董千里,2015)。而改善网络节点的资源配置和物流效率,可以有效支持物流枢纽所承载的城市经济高质量发展。中国物流业的迅速发展不仅依托微观网链的竞争力所创造的微观经济动能,还需要国家政策势能的支持与引导。2015年5月,商务部等部门发布了《全国流通节点城市布局规划(2015-2020年)》(以下简称流通节点城市政策),旨在培育一批具有较强集聚能力和辐射能力的流通节点城市,以实现流通节点城市生产效率的提升,进而带动东中西部地区流通网络协调发展。物流生产效率是由微观网链绩效集成起来的,而微观网链功能扩展是由交通运输基础设施构成的公共型网络支撑起来的,这就需要微观网链与宏观网络的对接、连接和一体化运作。政策规划的流通节点城市高度汇集了物流、资金流、信息流以及商流,其在流通网络中的枢纽地位对于提高流通节点城市物流生产效率具有重要意义。由此,这一现实的问题开始凸显:流通节点城市政策的实施是否促进了城市物流生产效率提升?政策实施带来城市物流生产效率的变化在东中西部地区会表现出同样的效果吗? 物流业作为国民经济运行和货物流通的重要支撑,其发展水平主要通过物流业效率来衡量(王琴梅等,2013)。关于物流业效率测算和实证研究,一些学者(范月娇,2015;范月娇等,2016;杨淇钧,2016;张中强,2012;袁丹等,2015;刘秉镰等,2010)利用随机前沿分析方法(SFA)进行物流业效率的测算。其中,范月娇(2015)通过随机前沿分析法测算物流业效率得出如下结论,产业结构和信息化水平是国家级流通节点城市物流业非效率的重要影响因素。还有一些学者(陈永平等,2018;余泳泽等,2010a;范月娇,2012;杨守德等,2016;曹炳汝等,2019)基于数据包络分析法(DEA)进行物流业效率的测算。其中,杨守德等(2016)利用数据包络分析法实证研究得出以下研究结论,流通节点城市流通效率与区域经济发展水平之间存在因果促进关系。物流政策是物流业的行动准则(杨铭,2011)。关于物流政策影响物流业效率的研究主要包括两方面:一是定性分析物流政策对物流业发展轨迹和实施效果的影响。王文举等(2017)研究了改革开放以来物流政策支持物流业发展的阶段性特点。其他学者研究发现,中国现行的物流政策本身存在缺陷(陈文玲,2009;林勇等,2006;赵娴,2006),并结合物流业发展存在的问题对今后物流政策的制定提出建议(赵娴等,2019)。二是物流政策对物流业发展影响的实证研究。Dou et al.(2014)基于政策模型来估计产业政策与物流发展的关系研究发现,政策是提高物流业效率的主要原因。范月娇(2015)研究认为,在物流政策颁布后,国家级流通节点城市物流业效率在空间维度上呈现中部地区城市略高于东部地区特征,而西部地区为最低。杨守德等(2016)研究指出,在物流政策背景下,区域流通节点城市流通效率对区域经济发展有显著影响。高安刚等(2019)运用双重差分法(Difference-In-Differences,DID)研究北部湾经济区政策颁布对物流业的影响,得出政策对地区物流业发展有正向影响的研究结论。 基于物流生产效率提升的现实需求,本文运用自然实验评估方法的双重差分模型,对政策实施和城市物流生产效率的关系进行实证检验,以挖掘城市物流生产效率的影响因素,并从东中西部地区城市的角度出发,考察政策对城市物流生产效率影响的异质性。双重差分法的使用有助于减少因遗漏变量等而造成的内生性问题,而运用多种方法进行稳健性检验使得研究结论要更为可靠。与现有文献研究相比,本文有如下贡献:首先,丰富现有物流政策类文献研究。目前,已有文献对物流政策的研究较多集中在对政策内容的梳理和评价方面,本文侧重研究政策实施对物流生产效率的净影响。其次,运用科学的方法检验物流政策和物流生产效率之间的关系。较多学者的研究集中在对国家或区域物流业效率的影响因素和实证研究方面,本文从城市物流业效率的研究出发,系统分析政策背景下流通节点城市物流生产效率的提升效应。 二、DID模型的构建与变量描述 (一)模型构建 双重差分模型由Ashenfelter et al.(1985)在1985年首次提出,该模型可有效解决实验组与控制组实验前的系统性差异,进而分析政策效果。其公式如下:
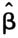
[,ols]=△
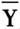
[,treat]-△
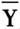
[,control]=(
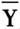
[,treat,2]-
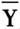
[,treat,1])-(
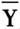
[,control,2]-
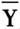
[,control,1]) (1)
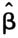 [,ols]=△
[,ols]=△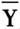 [,treat]-△
[,treat]-△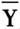 [,control]=(
[,control]=(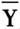 [,treat,2]-
[,treat,2]-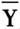 [,treat,1])-(
[,treat,1])-(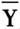 [,control,2]-
[,control,2]-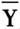 [,control,1]) (1)
[,control,1]) (1)