基于最大物流引力支撑树的区域物流协调发展决策研究

       一、引言

       区域物流的协调发展能够使得物流运作更加高效，城市间物流的带动效应更加显著，进而提高区域物流的发展水平，助力区域经济更好地发展。然而通常区域内节点城市较多，物流关系错综复杂，导致区域物流发展的针对性不强，物流运作效率低下，发展缓慢。因此，如何梳理区域内各节点城市间复杂的物流关系，识别区域内具有重要物流联系的节点城市关联，以对区域中节点城市的物流协调发展做出效果最显著的决策，是改善区域物流运作效率低下、物流发展步伐缓慢的有力举措。

       在区域物流协调发展的决策研究中，学者们主要是采用各类协调发展水平测度模型，对区域中节点城市的物流协调发展水平做出测度，根据测度原理分析测度结果，并从协调发展的薄弱环节出发，从宏观层面上定性做出区域物流协调发展的决策建议。张林等(2015)[1]采用多维灰色关联动态模型测度了全国21个节点城市的物流与经济的协调发展水平，并在测度结果的基础上以灰色关联度作为决策依据，对各节点城市的物流发展做出决策。张亚飞等(2019)[2]采用耦合协调度模型测度了“一带一路”沿线内陆节点城市的物流供需协调性，并基于此提出促进节点城市协调发展的决策建议。钱吴永等(2018)[3]采用复合系统协调度模型从静态及动态两个角度测度了全国21个节点城市的物流产业效率与经济增长间的协调关系，并提出了不同梯队节点城市的发展建议。林欣(2017)[4]综合考虑海峡西岸城市群的物流业关联度和发展协调度，提出了城市群的发展政策建议。彭会萍等(2018)[5]利用耦合协调度模型测度了区域物流及经济的协调发展水平，并在系统协同演化发展的趋势下，建立多元非线性规划模型对区域物流及经济的协调发展做出了决策性研究。定性定量相结合对区域物流协调发展做决策性研究的还有很多(弓宪文，2018；梁雯等，2017；梁雯等，2019；高康等，2019)[6-9]。但是这些文章更加侧重于以定量测度结果为准，定性分析物流协调发展薄弱环节所存在的问题，并给出提高物流协调发展水平的决策建议。鲜见有学者在优先识别出区域节点城市间物流关系的基础上，采用数学规划的方法对物流协调发展进行定量化决策研究。而通常明确区域中节点城市间的物流关系，能够辅助我们找到影响决策发展的关键联系。基于此进行定量化的决策，更能直观地体现出协调发展中的重点环节，发展建设的指向性将更加明确。

       本文创新性地引入物流引力来量化区域节点城市间的物流联系强度，并利用图论的方法梳理出区域节点城市中的强物流联系，通过构建两阶段决策模型对强物流联系节点城市间的物流发展做出定量化决策，以期为节点城市的物流发展给出有明确指向性的建议，同时兼顾节点城市间的发展联系，做到高效发展。

       二、模型及研究方法

       (一)引力模型

       引力模型源于牛顿的万有引力定律，即两物体间的引力与质量成正比，与其间的距离成反比。随后引力模型被移植于区域经济、区域物流中，研究节点城市间特定关系的联系强度。引力模型测度节点城市间的物流联系强度，基本公式如下：

       I[，ij]=GM[，i]M[，j]d[-r][，ij]

       (1)

       式中，I[，ij]为节点城市i，j间的物流引力；G为引力常数；M[，i]，M[，j]表示节点城市的物流质量；d[，ij]为节点城市i，j间的距离；r为引力衰减系数。通常，G取值为1，r取值为2，节点城市间的距离d通常选取各类交通运输线路中的最短距离。在对于节点城市质量的评价中，单一指标往往无法全面准确地衡量节点城市的质量，其质量应该是多指标综合的测度结果(李江苏等，2009)[10]。因此，在测度节点城市的物流质量时，应首先建立节点城市的物流评价指标体系，并采用加权系数法得到各节点城市的物流质量。

       以节点城市i为例，其物流质量M[，i]的计算公式如下：

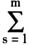       M[，i]=μ[，s]x[，si]

       (2)

       式中，μ[，s]为第s个物流指标的权重，采用熵权重法确定。x[，si]为节点城市i的第s个指标的归一化取值。

       (二)最大支撑树及Prim算法

       树图是无圈的连通图，一个网络图的最大支撑树能够连通该网络图中所有节点，且使连接节点的边权总和达到最大。文中采用Prim算法来搜索网络图中的最大支撑树。具体算法流程如下：###(1)从网络图中任选一个节点i，令i∈V，图中其余节点均包含在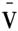中；

       (2)从V与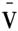的连线中找出权值最大的边，假设最大权值的边为[i，j]，则将该边计入最大支撑树内；

       (3)令V∩j→V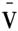，/j→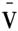；