基于个体移动轨迹的多中心城市引力模型验证

       1 引言

       反映空间相互作用的引力模型(又称重力模型、场强模型)是城市地理、城市规划的经典模型之一，在实践中有广泛应用[1-9]。但是由于缺乏实证，模型中的规模变量、距离衰减系数取值往往缺乏依据。从引力模型研究的经典文献来看并非如此，变量、系数取值有较严谨的实证。引力模型最早由Reilly提出，通过对Texas州大城市主要商场、家庭购物清单的“调查”发现两座城市之间的市场界限“大致”与人口规模呈正比、与距离的平方呈反比，据此“归纳”出了零售引力(Retail Gravitation)模型[10]。此后，Converse等对引力模型进行了演绎，分别提出了断裂点公式[11]和概率公式[12]，并用居民购物出行的调查数据做“实证”，经变量检验、参数校正后再将模型投入应用。说明在引力模型研究的早期阶段，研究者极为重视用实证数据验证模型。但此后可能是应用需求的增加，逐渐忽视了变量检验和参数校正；城市系统日趋复杂也加大了模型验证工作的难度。特别是模型中的距离衰减系数，当前在0.5-3.0之间取值已成为约定俗成的做法[13]，一般依据万有引力公式直接取2也不会受到质疑。而且现实中最初只针对居民前往商场购物出行的引力模型应用已经扩展到了就业通勤、信息联系、企业联系等[14-17]。

       随着城市的多中心化，小汽车普及、地铁线路成网使居民出行方式发生了显著改变。有学者提出这些变化是否“挑战了传统基于单中心假设的城市模型，空间是否依然存在逻辑？传统的地理空间的距离衰减性是否存在？”[18]。如果空间相互作用的规律已发生改变，那么需要重新审视引力模型应用的理论基础。随着数据存储、分析技术进步，为验证引力模型创造了条件。已有学者使用手机通话数据、浮动车GPS数据、企业工商注册数据等开展相关研究，证明了引力模型中的距离衰减规律依然存在[14-18]，其方法是以某一间隔距离汇总吸引量，再用幂函数拟合吸引量——距离曲线，如果拟合的幂函数曲线与实测结果有较高相关系数则表明吸引力衰减符合引力模型规律。还有学者更进一步，提出拟合幂函数的指数的绝对值就是距离衰减系数[15,17,19]，但是这一方法并未得到公认，而且指数是唯一值，掩盖了不同地区距离衰减的差异。与Huff当年的验证工作相比，验证的深度有待加强，验证的方法有待商榷。

       本文借助近年来出现的个体移动轨迹数据，用Huff当年的方法，对现在广泛应用的引力模型——Huff的引力模型进行验证。首先与Huff的验证内容一致，探讨在当前多中心城市中商业中心对居民购物出行的吸引力是否依然符合引力模型规律，特别是吸引力的距离衰减有何特征。随后针对模型应用扩展的现实需求，探讨就业中心对居民就业通勤的吸引力是否也同样符合引力模型规律，其距离衰减与购物出行的距离衰减特征有何差异。希望本文所做的验证工作能为日后引力模型得到更加严谨地应用提供帮助。

       2 引力模型验证方法和数据

       2.1 Huff的引力模型和验证方法

       Huff的引力模型是对Converse的断裂点公式的演绎，将非此即彼的市场区划分方法演进为居民受商业中心吸引的概率。并通过调查证明了居民选择购物目的地的比例符合引力模型规律；通过实测值——模拟值的拟合计算得到距离衰减系数，发现各商业中心到各社区的距离衰减系数从2.115-3.779不等，用拟合的距离衰减系数代入公式划分城市内部零售业商圈[12]。Huff的引力模型公式如下：

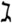       P[,ij]=S[,j]T[-][,ij]/∑[n][,j=1]S[,j]T[-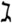][,ij] (1)

       ∑[n][,j=1]P[,ij]=1 (2)

       式中：P[,ij]为i社区属于商业中心j市场区的概率；S[,j]为商业中心j的规模；T[,ij]为i社区与商业中心j之间的距离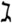；为距离衰减系数；n为商业中心的数量。

       模型中有两个变量(规模和距离)，一个参数(距离衰减系数)。Huff选取商业中心的面积作为规模变量；距离变量实测得到，以时间表示；距离衰减系数需要通过计算进行校正，具体方法为：①调查社区居民前往商业中心购物的人数，每个社区分别汇总，计算前往各商业中心的人数比例，这是实测值，有且只有一个结果；②将规模和距离变量代入模型，设定距离衰减系数的取值区间和精度将其逐一代入模型，计算得到每个社区属于各商业中心市场区的概率，这是模拟值(Huff并未说明距离衰减系数取值区间和精度，若从0.50取值到5.00，精度为0.01，则每个社区需要计算450个模拟值)；③逐一计算每个社区的实测值和模拟值的相关系数，相关系数最高的那个距离衰减系数就是该社区校正后的值；④计算每个社区的平均值得到校正后的距离衰减系数。本研究就使用该方法验证引力模型。

       2.2 研究范围、数据和空间单元