中图分类号：F235.99 文献标识码：A 文章编号：1004-972X(2019)11-0053-08 现代物流业连接经济生产和社会生活，也影响新旧动能转换的速度。现代物流业的健康发展对我国经济建设至关重要，我国多层次资本市场的快速发展，为现代物流业上市公司提供了更为广阔的融资平台。随着计算机技术、通信技术的发展，我国现代物流业快速发展，现代物流业上市公司的融资渠道进一步拓宽，融资效率对于现代物流业实现新旧动能转换和产业转型升级具有重要意义；然而由于资本市场体系不完善、银行信贷资源配置不够合理、部分现代物流企业内部管理问题等因素，使融资效率不足成为制约我国现代物流业发展的瓶颈问题。 对于融资效率理论的研究，国外学者侧重于融资结构和融资方式。美国经济学家Modiguani和Miller(1958)提出的融资结构理论(MM定理)认为，当不计所得税时，企业的市场价值与其融资结构不相关，并以此为基础，引入所得税对原有定理进行修正，强化其现实意义[1]。Myers和Nicholas(1984)提出了以逆向选择为基础的企业融资有序理论[2]。Jain和Kini(1994)对1979-1988年进行IPO的682家美国企业经营绩效进行研究，认为上市公司的经营业绩在IPO后普遍呈现下滑趋势，其股权融资效率较低[3]。Loughran和Ritter(1995)分析认为，增发新股的美国上市公司1970-1990年5年内的平均收益率远低于同期没有增发新股的上市公司[4]。国外学者对融资问题主要集中在融资理论的研究，虽然没有直接对融资效率进行研究，但为融资效率的研究奠定了理论基础。 对于融资效率的方法研究，美国运筹学家Charnes和Cooper(1978)提出的非参数目标决策法——数据包络分析(DEA)，该方法是对决策单元相对有效性进行评价的一种数量分析方法，其促进了效率评价理论的应用，是一种非参数法[5]。而随机前沿方法SFA是利用随机前沿生产函数进行效率估计，是一种参数方法。Fride(2002)提出三阶段DEA模型，认为在分析效率问题时，应剔除环境因素和随机误差的影响，进而对投入变量进行调整[6]。Avkiran和Rowlands(2008)认为通过三阶段DEA法，可以识别投入和产出的松弛变量，避免环境变量和随机误差的影响，得到融资效率更精准的值[7]。 国内关于融资效率的方法研究，主要有数据包络分析(传统DEA)、随机前沿分析(SFA)、灰色关联法、主成分分析法、模糊评价综合法等。徐淼和李薇(2010)采用主成分分析和模糊综合评价方法对融资效率进行分析，研究认为主成分分析方法在研究融资效率问题时，具有稳定性和操作性[8]。尚伟和杨芳芳(2011)采用主成分分析法和熵值法结合的方法对中小企业融资效率进行研究，认为中小板上市公司融资效率偏低，并且无行业相关性，建议通过多途径融资措施提高其融资效率[9]。田芬(2011)采用模糊数学的方法，针对企业融资的特性、各因素隶属度以及对比分析不同融资方式的融资效率差异[10]。朱玥颖(2017)运用三阶段DEA模型对2016年53家中国养老产业的融资效率进行了测算[11]；严复海和郭聪(2017)运用三阶段DEA模型对智能制造企业的融资效率进行了评估[12]。 关于产业融资效率的国外文献相对较少，而我国对产业融资效率的研究相对较多。目前学界开始重视现代物流业的融资问题的研究，然而采用定量方法的文献较少，且对比传统DEA模型，使用三阶段DEA方法对现代物流业的融资效率进行测度具有一定的现实意义。本文在新旧动能转换背景下，运用三阶段DEA方法，剔除外部环境因素的影响，可以得到更精准的现代物流业融资效率值，并寻求提高其融资效率的有效途径。 二、模型和方法 1.DEA模型 DEA模型(数据包络法)，是一种运用线性规划，用于评价决策单元效率的运筹学过程[13]，被广泛应用于融资效率问题的研究。在融资效率的研究中，由于企业面临不同的环境，因此传统DEA模型不能鉴别融资效率的高低是企业自身原因还是受环境影响。 本文综合考虑现代物流企业经营环境差异和随机因素，采用三阶段DEA模型，第一阶段计算DEA初始融资效率值，第二阶段对其进行SFA回归，剔除环境因素的影响，并在第三阶段得到调整后的融资效率值。 2.三阶段DEA效率评价模型 第一阶段：采用传统DEA模型分析初始融资效率，选择投入导向的BCC模型。表示为：
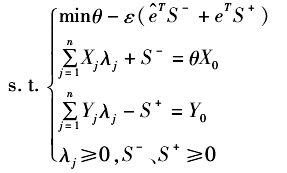
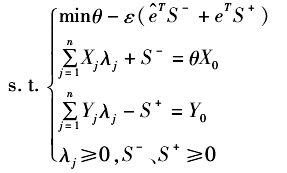其中，j=1，2，…，n，表示决策单元；X、Y表示投入、产出向量。 若θ=1，S[+]=S[-]=0，则决策单元DEA有效； 若θ=1，S[+]≠0，或S[-]≠0，则决策单元弱DEA有效； 若θ<1，则决策单元非DEA有效。 决策单元效率值受管理无效率、环境因素和统计噪声的影响，需要对三种影响进行分离。 第二阶段：似SFA回归剔除环境因素和统计噪声。 第二阶段需要将第一阶段的松弛变量分解成环境因素、管理无效率和统计噪声效应，借助于SFA回归，构造如下类似SFA回归函数： S[，ni]=f(Z[，i]；β[，n])+v[，ni]+μ[，ni]，i=1，2，...，I；n=1，2，...，N 其中，Z[，i]是环境变量，β是环境变量的系数；S[，ni]表示第ni个决策单元，第n项投入的松弛值；v[，ni]+μ[，ni]是混合误差项，v[，ni]表示随机干扰，μ[，ni]表示管理无效率。 为了剔除环境因素和随机因素对效率的影响，便于将各决策单元调整于相同的外部环境中。
