中图分类号:F061.5 文献标识码:A 文章编号:1003-5230(2019)04-0089-11 党的十八大以来,我国区域经济一体化进程不断加快,已形成长江三角洲区域一体化、京津冀协同发展、长江经济带发展、粤港澳大湾区建设的四大跨区域协调发展的总体格局。长江经济带覆盖上海、江苏、浙江、安徽、江西、湖北、湖南、重庆、四川、云南、贵州等11省市,面积约205万平方公里,占全国的21%,人口和经济总量均超过全国的40%[1]。长江经济带区位条件优越,综合实力较强、生态地位重要、发展潜力巨大。2016年,中共中央政治局审议通过了《长江经济带规划纲要》,确立了以共抓大保护、不搞大开发为导向推动长江经济带发展,建立长江经济带“一轴、两翼、三极、多点”的发展新格局。“一轴”是以长江黄金水道为依托,发挥上海、武汉、重庆的核心作用;“两翼”分别指沪瑞和沪蓉运输通道,增强南北两侧腹地重要节点城市人口和产业集聚能力;“三极”指的是长江三角洲、长江中游和成渝3个城市群,打造长江经济带的三大增长极。“多点”是指充分发挥三大城市群以外地级城市的支撑作用,加强与中心城市的经济联系与互动,带动区域经济发展。长江中游城市群是长江经济带的重要组成部分,包括湖北、湖南、江西3省的31个城市,土地面积约32.61万平方公里,总人口和地区生产总值均超过了长江经济带的20%。长江中游城市群交通便利、工业体系完备、产业基础良好、人才储备丰富,是实施和促进中部地区崛起和长江经济带战略的重点区域,在我国区域经济发展格局中具有重要的战略地位。 随着我国经济持续快速增长,物流产业已经成为国民经济的支柱产业之一。城市群经济的不断发展催生了区域内大量的物流需求,为区域内物流产业发展提供了动力。另一方面,物流产业作为城市群内的基础性产业,对城市群内其他产业的发展起着重要的推动作用,能有效提升城市群经济发展水平。因此,城市群内物流产业与区域经济如何协调发展,成为提升城市群竞争力的重大课题。 已有文献主要运用下列几种方法对物流产业与经济发展的关系展开研究。第一,通过构建计量经济学模型,研究物流产业与经济发展的相关性。聂正彦和李帅通过面板分位数回归,分析物流业对我国区域经济增长的影响,发现物流业对经济增长的影响存在明显的跨区差异[2]。叶柏青等应用哈肯模型对我国29个省(市、区)的面板数据进行分析,发现我国经济发展水平与物流业的发展状况存在较高的协同性[3]。田越和杨萌运用VAR向量自回归,分析了山西物流业发展与区域经济增长的互动关系,结果表明山西省物流业发展较为滞后,对经济增长促进作用较小[4]。第二,通过耦合协调度模型,计算物流产业与经济发展的耦合协调度,分析两者的协调程度。李军通过耦合协调度模型研究了我国省级区域的物流与经济协调发展程度[5]。郭湖斌和齐源计算了长三角地区物流与经济的耦合协调度,分析了两者的耦合关系[6]。高康等分析了泛珠三角区域物流与经济耦合协调程度的演变[7]。第三,通过空间经济学模型研究物流产业与经济发展的空间分布特征。李剑和姜宝运用空间计量模型分析了中国内地31个省(市、区)物流产业集聚对区域经济增长的影响,发现物流产业聚集对第三产业贡献较大,对第一产业贡献不显著[8]。侯海涛应用空间经济学方法,对河南省物流与经济集聚进行了空间计量分析[9]。 从以上文献可以看出,现有研究多以省域或东南沿海地区的城市群为研究对象,鲜有学者对长江中游城市群的物流产业与经济发展协同性开展研究。现有研究中对耦合协调度的计算方法存在较大差异,不同方法计算出的耦合协调度存在较大差异。本文以长江中游城市群中的31个城市为研究对象,通过采集城市群内各城市的物流与经济发展水平基本数据,构建区域物流系统和区域经济系统,结合熵值法建立区域物流与区域经济之间的耦合模型,计算物流与经济的耦合协调度,分析两者间的协调发展程度,并提出相应的对策与建议。 二、理论分析与模型构建 耦合是物理学中的概念,用来描述两个及以上相关系统相互作用、相互影响的程度。正向耦合表明系统间相互促进,协调发展。负向耦合则说明系统间相互摩擦,相互掣肘。已有研究表明[5][6][7][10][13][14],区域内的物流和经济两个系统存在一定的耦合关系,区域内物流产业的发展能提升企业供应链效率,降低物流成本,从而提升企业的利润水平,进一步推动社会经济发展。而经济发展会产生产业集聚效应,催生大量的物流需求,带动物流行业发展,同时产业集聚也会使地方财政收入增加,地方政府能加大对交通设施、技术研发、人才培养等方面的投入,从而反哺物流产业的发展,具体耦合关系如图1所示。
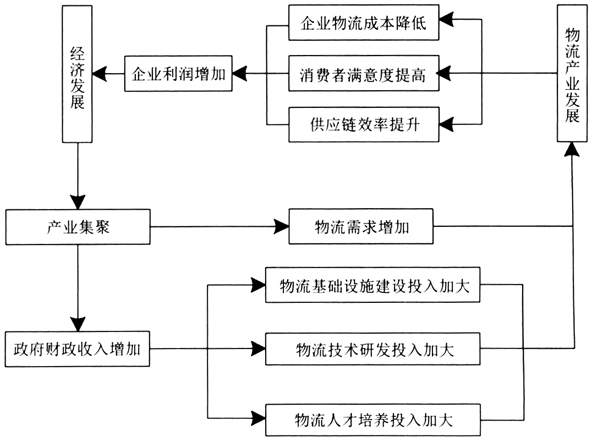
图1 物流产业与经济发展耦合关系 学术界一般用耦合度来度量系统间耦合作用的强度,耦合度高表明系统间呈现出正向耦合,反之则负向耦合,已有研究中,部分学者使用式(1)计算耦合度[7][11][12]。 c=
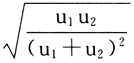
(1) 式(1)中u[,1]、u[,2]为经过标准化处理后的两个系统的评价指数,0≤u[,1]≤1且0≤u[,2]≤1。c为两者的耦合度,根据大部分已有研究中对耦合度的定义[6][10][11][12][13][14],c的取值范围应为0≤c≤1,当c的值为0时,u[,1]和u[,2]无耦合性;当c的值为1时,两者的耦合度达到最大。但若采用式(1)计算耦合度c,则计算得出的c的取值范围为0≤c≤0.5,与学术界对耦合度的普遍定义不一致,且后续研究中通过c计算出的耦合协调度D的取值范围将为0≤c≤
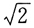
/2,不利于建立评价体系。因此,为了使c的取值范围为0≤c≤1,部分学者采用下列式(2)来计算耦合协调度[13][14]。
 图1 物流产业与经济发展耦合关系 学术界一般用耦合度来度量系统间耦合作用的强度,耦合度高表明系统间呈现出正向耦合,反之则负向耦合,已有研究中,部分学者使用式(1)计算耦合度[7][11][12]。 c=
图1 物流产业与经济发展耦合关系 学术界一般用耦合度来度量系统间耦合作用的强度,耦合度高表明系统间呈现出正向耦合,反之则负向耦合,已有研究中,部分学者使用式(1)计算耦合度[7][11][12]。 c=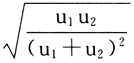 (1) 式(1)中u[,1]、u[,2]为经过标准化处理后的两个系统的评价指数,0≤u[,1]≤1且0≤u[,2]≤1。c为两者的耦合度,根据大部分已有研究中对耦合度的定义[6][10][11][12][13][14],c的取值范围应为0≤c≤1,当c的值为0时,u[,1]和u[,2]无耦合性;当c的值为1时,两者的耦合度达到最大。但若采用式(1)计算耦合度c,则计算得出的c的取值范围为0≤c≤0.5,与学术界对耦合度的普遍定义不一致,且后续研究中通过c计算出的耦合协调度D的取值范围将为0≤c≤
(1) 式(1)中u[,1]、u[,2]为经过标准化处理后的两个系统的评价指数,0≤u[,1]≤1且0≤u[,2]≤1。c为两者的耦合度,根据大部分已有研究中对耦合度的定义[6][10][11][12][13][14],c的取值范围应为0≤c≤1,当c的值为0时,u[,1]和u[,2]无耦合性;当c的值为1时,两者的耦合度达到最大。但若采用式(1)计算耦合度c,则计算得出的c的取值范围为0≤c≤0.5,与学术界对耦合度的普遍定义不一致,且后续研究中通过c计算出的耦合协调度D的取值范围将为0≤c≤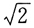 /2,不利于建立评价体系。因此,为了使c的取值范围为0≤c≤1,部分学者采用下列式(2)来计算耦合协调度[13][14]。
/2,不利于建立评价体系。因此,为了使c的取值范围为0≤c≤1,部分学者采用下列式(2)来计算耦合协调度[13][14]。