中图分类号:F505 文献标识码:A 文章编号:1001-4098(2018)06-0109-08 1 引言 第四方物流(Forth Party Logistics,4PL)是以供应链整合为目的的现代物流运作模式[1]。4PL的特点决定了它具备协同多家第三方物流(Third Party Logistics,3PL)为客户定制配送方案的能力。在这一过程中,4PL根据客户提出的要求定制配送方案。最终达到客户、3PL供应商以及4PL供应商“三赢”的目的。 时变4PL路径问题(4PL Routing Probem on the Time Varying Networks,4PLRPTVN)是4PL路径优化问题的扩展。在已有研究中,一般将两节点间的运输时间视为恒定的[1-4],或者视为不确定的[5-7]。但在实际应用中,不同时段上车辆流量的不同会造成车辆行驶速度具有随“时间段”变化的特点。而4PL负责的往往是跨区域的任务,具有行程远、运期长等特点。因此,在相应的运输时间内,由于天气状况、交通条件、运输淡旺季等原因使得4PL的运输时间具有时变性。 对于时变网络,运输商在不同时间段通过相同路径可能会产生不同的运输时间,从而导致不同的运输费用。对于4PLRPTVN,如果3PL可以在节点等待,那么即使要为“等待”付出一定的费用,也有可能节省总的运输成本。等待时变问题在4PLRP研究中仍是一个新的领域,但是在其他优化问题中。这一问题已有涉及。例如:Cai等[8]对时变条件下允许等待的最短路径问题进行了研究。辛春林等[9]针对时变条件下多式联运危险品路径优化问题,建立了时变条件下危险品多式联运的最短路径选择模型。Wen等[10]针对实际路况信息,提出了求解时变网络下的费用最短路算法,并针对伦敦市的实际路况信息进行了测试。 以上成果为4PLRPTVN的研究打下坚实基础。但是在已有研究中,等待时间一般假设具有上限或通过约束加以限制。实际上,由于交货期的存在,各节点的等待时间是有上限的。因此,本文基于时变网络,在考虑节点等待的前提下,首先建立了考虑货物等待成本、3PL供应商停靠与转换成本的4PLRPTVN数学规划模型。然后,给出了各节点等待时间及时变网络下运输时间的计算方法。设计了基于K-短路算法的混合粒子群算法(K-PSO)以及用于对比的基于剪枝策略的亚启发式算法(简称剪枝算法)。最后,在实验分析中,针对不同节点数目下和不同3PL供应商数目下的实例计算,以及与剪枝算法和遗传算法[7]的对比分析说明本文所提K-PSO算法在处理4PLRPTVN的优势;表明了运输过程中的适当等待不仅不会延长交货时间反而会节省总的运输费用。 2 问题描述及模型 2.1 问题描述 假设某4PL供应商拟承揽一项具有交货期的运输任务。在运输过程中,4PL需要将该任务在不同路段上的运输工作委托给3PL供应商,并且假设3PL的运输速度是时变的。如果4PL在相邻路径上使用相同的3PL供应商,那么4PL只需要支付3PL在中转节点的停靠费用并记录停靠时间,否则还需要支付转运费用并计算转运时间。为了避免3PL在运输时间较长的时间段出发,4PL还可以指定3PL在起始或各中转节点的出发时间,但4PL也要为此支付一定的“等待”费用。 将上述问题看作由n个节点r重边组成的多重图,于是得到如图1所示的4PLRPTVN运输网络。(其中,V(|V|=n)为节点集,为边集,两点间边的编号对应可承担任务的3PL供应商的序号。)
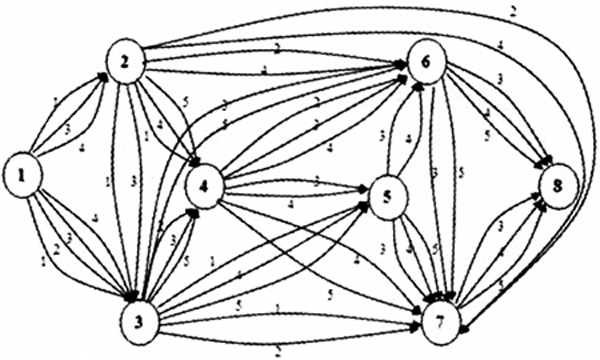
图1 4PLRP网络多重图

2.2 数学模型 根据以上分析,建立的模型如下:
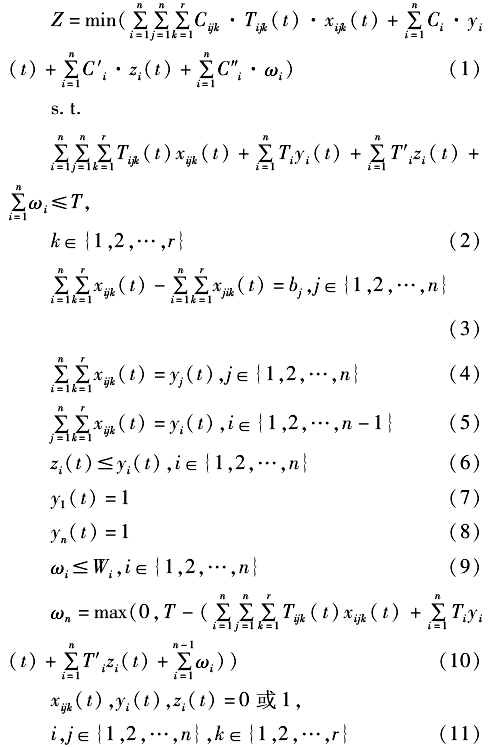
其中,式(1)为目标函数,表示3PL在运输途中、在转运节点停靠、在转换和等待时的费用总耗;式(2)表示到达目的地的时间不大于客户要求的时间;式(3)表示网络流流量平衡;式(4)、式(5)表示选择的点是从起点到目的节点的通路;式(6)表示如果在i点转换3PL供应商则一定在i点中转;式(7)、式(8)分别表示路径的起始和终止节点;式(9)表示决策变量
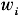
在各节点的等待时间不大于该节点的最大等待时间
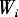
(
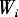
的确定见3.1节);式(10)表示提前到达终点时的存储时间;式(11)表示
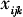
(t),
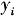
(t)和
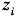
(t)为0-1变量。
 图1 4PLRP网络多重图
图1 4PLRP网络多重图  2.2 数学模型 根据以上分析,建立的模型如下:
2.2 数学模型 根据以上分析,建立的模型如下: 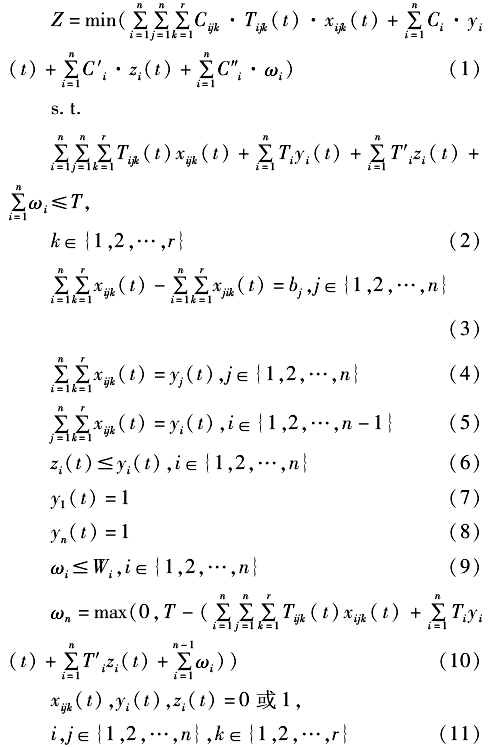 其中,式(1)为目标函数,表示3PL在运输途中、在转运节点停靠、在转换和等待时的费用总耗;式(2)表示到达目的地的时间不大于客户要求的时间;式(3)表示网络流流量平衡;式(4)、式(5)表示选择的点是从起点到目的节点的通路;式(6)表示如果在i点转换3PL供应商则一定在i点中转;式(7)、式(8)分别表示路径的起始和终止节点;式(9)表示决策变量
其中,式(1)为目标函数,表示3PL在运输途中、在转运节点停靠、在转换和等待时的费用总耗;式(2)表示到达目的地的时间不大于客户要求的时间;式(3)表示网络流流量平衡;式(4)、式(5)表示选择的点是从起点到目的节点的通路;式(6)表示如果在i点转换3PL供应商则一定在i点中转;式(7)、式(8)分别表示路径的起始和终止节点;式(9)表示决策变量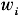 在各节点的等待时间不大于该节点的最大等待时间
在各节点的等待时间不大于该节点的最大等待时间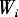 (
(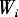 的确定见3.1节);式(10)表示提前到达终点时的存储时间;式(11)表示
的确定见3.1节);式(10)表示提前到达终点时的存储时间;式(11)表示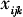 (t),
(t),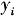 (t)和
(t)和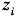 (t)为0-1变量。
(t)为0-1变量。