如何将学科核心素养落实到课堂,是教育工作者面临的一个重要课题.某地区对数学教师的统计数据表明:对逻辑推理、数学运算和数学建模的关注度超过90%,而对数学抽象的关注度仅为18%.这一现象有一定的普遍性,数据反映了该地区数学教师对数学抽象素养重视不够,也说明在课堂上落实数学抽象素养存在一定的困难. 数学抽象是数学学科六大核心素养之一.数学抽象是指通过对数量关系与空间形式的抽象得到数学研究对象的素养,包括从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系,从事物的具体背景中抽象出一般规律和结构,并用数学语言予以表征.数学抽象是数学的基本思想,反映了数学的本质特征,贯穿于在数学产生、发展、应用的过程中. 章建跃先生认为,从数学知识发生、发展过程的合理性和学生思维过程的合理性上加强思考,是落实数学学科核心素养的关键点.为了解决“两个合理性”,需要为数学抽象寻找恰当的载体.问题情境是一个重要的载体,对问题某一方面的特征进行抽象,一般问题的个数不小于3.我们知道,问题有主次、并列之分,情境也类似.我们把在某一个过程中起关键或主要作用的情境称为主情境,其他情境称为辅助情境.对某一个概念进行数学抽象,要根据其特点,设置主辅情境、系列情境或单个情境.情境是为了数学,活动是为了思考,这就是情境的意义所在. 下面通过对教材中几个难点概念的分析、改进和创造,探索在数学抽象过程中建构情境的方法,进而提出问题. 一、创设主辅情境,让学生提出问题,助力发展数学抽象素养 对于创设的主辅情境,主情境要尽可能使用真实情境.这里所说的真实情境,指的是情境要源于学生的生活实际(现实情境),要与学生的经验相联系(学习情境).对于学生而言,这样的情境真实可感,容易产生研究问题的“愤”“悱”与好奇,促使学生发现问题、提出问题. 案例1:参数方程的意义. 教材情境:在建立了平面直角坐标系和极坐标系之后,平面上任意一点的位置都可以用一组有序数对确定,平面上的曲线也可以用方程f(x,y)=0或φ(ρ,θ)=0表示.随着对曲线研究的深入,在很多情况下,要建立曲线上的点的坐标之间的直接关系比较困难.例如,当物体做斜抛运动时,它的运动轨迹不仅受到初速度的影响,还受到重力的影响.在物理学中,我们已经知道它的轨迹是一条抛物线.如果还要考虑水平方向的阻力,它的运动轨迹就成为如图1所示的弹道曲线.
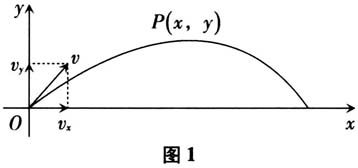
参数方程的意义是学生在高二学习的内容,在此之前已经学习过圆锥曲线的方程.圆锥曲线的方程反映了变量x,y的直接联系,而参数方程则反映了变量x,y的间接联系.因此,可以创设“学习参数方程的必要性”的情境,之后再提出恰当的问题. 教材中的弹道曲线无疑是一个很好的情境,但是仅靠这一个情境让学生理解“为何要学习参数方程”仍有困难,也不利于发展学生的数学抽象素养.如果用三个情境,则耗时过多.在名师工作室的一次教学研讨活动中,一位青年教师设置了如下主辅情境. 情境1(主情境):大家都喜欢玩游戏.现在有一个关于“弹弓”的主题游戏,调整弹弓的角度,将子弹以5 m/s的初速度水平抛出,子弹的运动轨迹如图2所示.假设子弹距地面的高度为1m,g取10
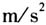
.

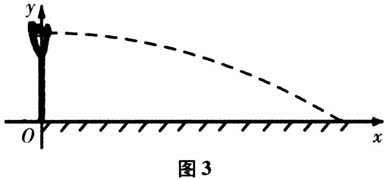
师:在这个情境中,你能提出哪些数学问题? 课堂上有几名学生分别提出下列问题:这颗子弹经过多长时间落地?这颗子弹的落地点与弹弓的水平距离为多少?子弹的运动轨迹是一条抛物线,求子弹运动的轨迹方程. 师(追问):哪一个是核心问题呢? 通过讨论,学生觉得核心问题是子弹运动的轨迹方程.教师让学生尝试求解子弹运动的轨迹方程. 问题1:子弹运动的轨迹方程是什么? 生:建立平面直角坐标系,如图3所示.设子弹运动轨迹上任意一点的坐标为P(x,y),子弹t时刻的位置为
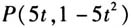
,所以
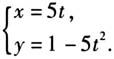
.
师:不难发现,方程组
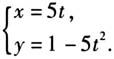
.中的x与t,y与t都是函数关系.
 参数方程的意义是学生在高二学习的内容,在此之前已经学习过圆锥曲线的方程.圆锥曲线的方程反映了变量x,y的直接联系,而参数方程则反映了变量x,y的间接联系.因此,可以创设“学习参数方程的必要性”的情境,之后再提出恰当的问题. 教材中的弹道曲线无疑是一个很好的情境,但是仅靠这一个情境让学生理解“为何要学习参数方程”仍有困难,也不利于发展学生的数学抽象素养.如果用三个情境,则耗时过多.在名师工作室的一次教学研讨活动中,一位青年教师设置了如下主辅情境. 情境1(主情境):大家都喜欢玩游戏.现在有一个关于“弹弓”的主题游戏,调整弹弓的角度,将子弹以5 m/s的初速度水平抛出,子弹的运动轨迹如图2所示.假设子弹距地面的高度为1m,g取10
参数方程的意义是学生在高二学习的内容,在此之前已经学习过圆锥曲线的方程.圆锥曲线的方程反映了变量x,y的直接联系,而参数方程则反映了变量x,y的间接联系.因此,可以创设“学习参数方程的必要性”的情境,之后再提出恰当的问题. 教材中的弹道曲线无疑是一个很好的情境,但是仅靠这一个情境让学生理解“为何要学习参数方程”仍有困难,也不利于发展学生的数学抽象素养.如果用三个情境,则耗时过多.在名师工作室的一次教学研讨活动中,一位青年教师设置了如下主辅情境. 情境1(主情境):大家都喜欢玩游戏.现在有一个关于“弹弓”的主题游戏,调整弹弓的角度,将子弹以5 m/s的初速度水平抛出,子弹的运动轨迹如图2所示.假设子弹距地面的高度为1m,g取10  .
.  师:在这个情境中,你能提出哪些数学问题? 课堂上有几名学生分别提出下列问题:这颗子弹经过多长时间落地?这颗子弹的落地点与弹弓的水平距离为多少?子弹的运动轨迹是一条抛物线,求子弹运动的轨迹方程. 师(追问):哪一个是核心问题呢? 通过讨论,学生觉得核心问题是子弹运动的轨迹方程.教师让学生尝试求解子弹运动的轨迹方程. 问题1:子弹运动的轨迹方程是什么? 生:建立平面直角坐标系,如图3所示.设子弹运动轨迹上任意一点的坐标为P(x,y),子弹t时刻的位置为
师:在这个情境中,你能提出哪些数学问题? 课堂上有几名学生分别提出下列问题:这颗子弹经过多长时间落地?这颗子弹的落地点与弹弓的水平距离为多少?子弹的运动轨迹是一条抛物线,求子弹运动的轨迹方程. 师(追问):哪一个是核心问题呢? 通过讨论,学生觉得核心问题是子弹运动的轨迹方程.教师让学生尝试求解子弹运动的轨迹方程. 问题1:子弹运动的轨迹方程是什么? 生:建立平面直角坐标系,如图3所示.设子弹运动轨迹上任意一点的坐标为P(x,y),子弹t时刻的位置为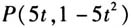 ,所以
,所以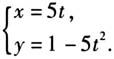 .
.  师:不难发现,方程组
师:不难发现,方程组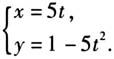 .中的x与t,y与t都是函数关系.
.中的x与t,y与t都是函数关系.