现代认知心理学认为,学习是学习者以信息的输入、编码为基础,根据已有经验及认知结构,主动建构内部的心理表征,进而获得心理意义的过程.数学学习是对学生知识、技能、概念、法则在心理上组织起恰当的有效认识结构,使之成为个人内部的知识网络的一部分.数学学习水平的层级划分对数学教学有着不容忽视的意义. 一、设计的背景 函数是贯穿高中数学课程的主线,而复合函数作为函数知识的重要组成部分,是历年高考的热门考点.同时,复合函数与导数、不定积分等有密切的联系,是数学学习的基础.理解复合函数的概念及性质,对数学学习有着举足轻重的作用,有助于学生进一步完善数学知识结构. 从数学必修一开始,不少习题就与复合函数有密切的联系.然而,人教版高中教材中关于复合函数的概念直到选修2-2才正式给出,并且是一种描述性的定义,还不能算是严格定义.许多教师在教学时只是简单介绍这一定义及其常用性质,不少学生对复合函数的理解只是知其表面形式,经不起推敲,对其单调性的判断方法“同增异减”更是云里雾里,停留在机械记忆的阶段. 虽然受高中生认知水平的局限,我们不可能要求学生严谨地理解复合函数的本质,但如果教学中能采取适当的方法,将会有助于复合函数这一难点的学习. 二、设计的理念 根据皮亚杰的建构主义学习理论,本设计以学生为主体,利用信息技术,融入数学实验活动,为学生理解复合函数知识搭建“脚手架”. 三、设计的创新之处 (一)选题具有价值 复合函数的教学至关重要,然而现阶段,针对复合函数知识理解的实证研究非常少.因此,以复合函数为选题,创新教学设计,具有教学价值. (二)教学手段新颖 充分使用现代信息技术,利用各种丰富的感性材料,引领学生主动参与、发现、探究、解决问题,从而深化学生对复合函数知识的理解,开发学生的创新潜能. (一)教学背景 【教学对象】中等水平及以上学校的高一学生. 【课时安排】40分钟. 【学情分析】 (1)认知基础:学生已学习过函数的相关概念及其性质,能理解映射的含义,具备用定义法判断函数单调性的能力. (2)认知障碍:外函数与内函数的分辨,复合函数几何意义的理解. 【教学目标】 (1)知识与技能 ①理解复合函数的概念; ②了解复合函数的几何意义; ③理解用“同增异减”方法判断复合函数单调性的内涵,会用“同增异减”求复合函数的单调区间. (2)过程与方法 通过参与发现、探究、分析、归纳等数学活动,理解复合函数,体会“同增异减”的内涵. (3)情感态度价值观 在主动参与数学活动的过程中,提高自信心,增强数学学习的兴趣. 【教学重点】复合函数的概念、“同增异减”的内涵; 【教学难点】中间变量、外函数及内函数三者的辨别、复合函数的几何意义; 【教学方法】引导探究法 【教学工具】几何画板、MATLAB、PPT (二)教学过程设计 1.创设情境,引入新知 (1)我们已经学习了函数的概念:设A,B是两个非空数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数y和它对应,称f:A→B为从集合A到集合B的一个函数,记为y=f(x),x∈A. 函数是两个集合之间的对应关系.常见的函数如
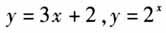
,都可以轻易地找到这种对应关系,画出函数图象.但有时候,我们遇到的函数的形式比较复杂,比如
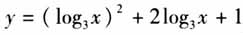
,函数图象不容易画出来,那么,如何确定这种函数的性质呢? 设计意图 提出问题,激发学生产生弥补“心理缺口”的学习动力. (2)引导学生观察发现,x都是以
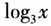
的形式出现,如果设
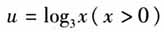
,则
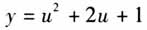
,变成我们比较熟悉的二次函数的形式.这样,通过在x,y之间搭一座桥u,我们化复杂为简单. (3)提出疑问:这座桥的建立是否合理?建了这座桥之后又可以带来一些怎样的便利?有什么新发现?
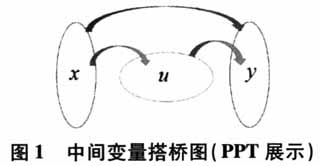
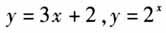 ,都可以轻易地找到这种对应关系,画出函数图象.但有时候,我们遇到的函数的形式比较复杂,比如
,都可以轻易地找到这种对应关系,画出函数图象.但有时候,我们遇到的函数的形式比较复杂,比如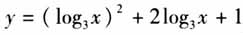 ,函数图象不容易画出来,那么,如何确定这种函数的性质呢? 设计意图 提出问题,激发学生产生弥补“心理缺口”的学习动力. (2)引导学生观察发现,x都是以
,函数图象不容易画出来,那么,如何确定这种函数的性质呢? 设计意图 提出问题,激发学生产生弥补“心理缺口”的学习动力. (2)引导学生观察发现,x都是以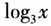 的形式出现,如果设
的形式出现,如果设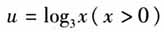 ,则
,则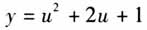 ,变成我们比较熟悉的二次函数的形式.这样,通过在x,y之间搭一座桥u,我们化复杂为简单. (3)提出疑问:这座桥的建立是否合理?建了这座桥之后又可以带来一些怎样的便利?有什么新发现?
,变成我们比较熟悉的二次函数的形式.这样,通过在x,y之间搭一座桥u,我们化复杂为简单. (3)提出疑问:这座桥的建立是否合理?建了这座桥之后又可以带来一些怎样的便利?有什么新发现? 