0 引言 公路运输是中国货物运输的主要方式,1984-2015年,中国公路货运量占货运总量的比例均在70%以上;1984-2007年,公路货物周转量占货物周转总量的比例一直维持在10%-15%之间,2008-2015年,这一比例增加到了30%以上[1]。然而,我国公路物流业较发达国家落后近20年,车辆空驶率达40%以上,对环境、能耗、交通基础设施等的负面影响巨大。实业界普遍认为公路物流目前存在的突出问题是“小、散、乱、差”。“小”:指的是经营主体规模小、数量多。全国公路物流企业有750多万户,平均每户仅拥有货车1.5辆。“散”:指的是经营运作处于“散兵游勇”状态,产业的组织化水平很低,90%以上的运力掌握在个体运营司机手中,行业集中度仅为1.2%左右。“乱”:指的是市场秩序较乱,竞争行为不规范,诚信体系缺失。“差”:指的是服务质量差,经营效益差。这些现象背后隐藏着一系列根本性的问题,即:公路物流资源的配置效率怎样,各省(自治区、直辖市)之间有无差异?影响公路物流效率的主要因素有哪些?为回答这些问题,本文将首先通过建立非径向超效率DEA模型和TOPSIS效率测度模型,分别按地区测算出公路物流效率值并进行比较,探讨不同测度方法下中国公路物流效率的地区差异性;其次,通过建立面板回归模型,分析中国公路物流效率的主要影响因素。文章内容安排如下:接下来第二部分为文献综述,第三部分为模型与方法,第四部分为数据、指标选取,第五部分为实证结果和分析,最后为结论与政策建议。 1 文献综述 国外专门研究公路物流效率的文献较少,Oum等[2]最早提出了交通生产率的概念,并探讨了不同的测算方法;Léonardi等[3]研究了德国公路物流的能源效率问题;Kumar[4]研究了印度道路运输业技术效率及决定因素。Jarboui等[5]利用随机前沿方法对18个国家54个公共道路运输经营者的技术效率进行了测量,并利用Tobit模型对其影响因素进行了研究。Pal和Mitra[6]利用数据包络分析法的定向距离函数,测量了2012-2013年印度37个道路运输组织的技术效率。国内方面,王亚华等[7]采用Malmquist-DEA方法测算了中国交通全行业及四个主要部门1980-2005年间的生产率变动,并引入Bootstrap-DEA方法对效率测度进行纠偏。刘玉海等[8]采用非参数DEA的Malmquist生产力指数方法,发现2000-2004年中国道路运输业营运效率生产力总体上呈现出改善的态势。段新等[9]通过建立DEA模型对中国公路运输效率进行评价,发现中国公路运输效率存在显著的地域差异,半数省份DEA有效,三分之二的地区达到规模效益递减或不变,公路物流资源过度投入和使用效率低下严重制约运输效率的提高。杨良杰等[10]引入非期望产出模型SBM-Undesirable,评价了1997-2010年中国公路运输效率,发现中国公路物流效率水平整体偏低,且存在显著的区域差异性。宋敏等[11]运用DEA规模可变—产出导向模型测算了我国2001-2011年公路投资效率。张天华等[12]研究了中国交通基础设施建设对企业资源配置效率的影响及其作用机制。张毅等[13]以山西公路客运企业为例,基于半参数随机成本前沿方法研究了道路运输企业成本无效率问题。张毅等[14]通过不同的随机成本前沿模型,分析了山西省37家公路客运企业2010-2014年的成本效率。 从以往研究来看,国外学者主要从能耗、环境、公共交通等为切入点研究公路交通行业效率问题,国内学者近些年来结合中国国情,对中国交通运输业运行效率的实证研究逐步增多,但仍存在以下不足:一是研究内容方面,绝大多数学者从交通运输业或道路运输业的整体视角出发,将货物和旅客运输作为一个研究对象考虑,由于二者在运载工具、从业人员数量、管理方式等方面均存在较大差异性,混合测算出的公路运输效率并不能精确反映公路货物运输效率;二是研究方法方面,DEA分析对于异常值非常敏感,稳定性较差,即使运用随机前沿和固定前沿测度效率,不同决策单元效率的计算结果也有很大差异,而且传统DEA尽管保证了数据包络曲线的凸性,但同时也可能造成投入要素的拥挤或松弛,采用单一方法测度效率的准确性不高。因此,本文将克服以上不足,选取中国公路货物运输相关数据,采用组合效率测度方法,对中国公路物流效率及其影响因素进行深入剖析。 2 模型与方法 2.1非径向超效率DEA模型 DEA是评价效率和生产率的常用方法之一,该方法直接使用样本数据(即决策单元的输入、输出数据)便可以测算出相对效率值。DEA方法是Charnes等人[15]在Farrell(1975)关于生产效率研究的基础上提出的一种系统分析方法,建立的CCR模型可以用来评价部门间的相对有效性。已有许多数据规划DEA相关的扩展模型被提出,测度方法趋于成熟,并形成一套庞大的效率测度体系。在DEA效率分析中,不论是CCR模型或是BCC模型,往往存在多个决策单元的效率值为1的情况,此时决策单元效率值之间无法比较。对此,Andersen(1993)[16]提出了超效率模型,克服了之前模型的缺陷。具体模型如下:
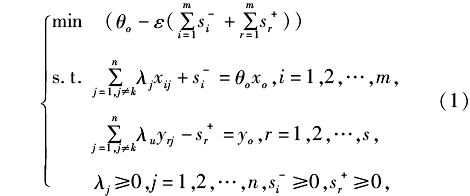
式(1)中,
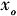
表示第o个决策单元的第i种投入,
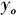
表示第o个决策单元的第r种产出,m表示产出数量,s表示投入数量,n表示决策单元数量,ε表示非阿基米德无穷小量。利用该模型,能够对所有DEA决策单元进行排序[17-18]。
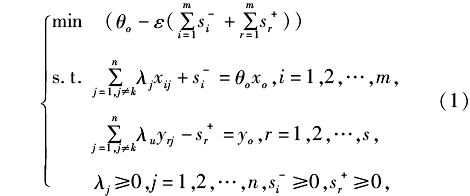 式(1)中,
式(1)中,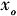 表示第o个决策单元的第i种投入,
表示第o个决策单元的第i种投入,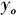 表示第o个决策单元的第r种产出,m表示产出数量,s表示投入数量,n表示决策单元数量,ε表示非阿基米德无穷小量。利用该模型,能够对所有DEA决策单元进行排序[17-18]。
表示第o个决策单元的第r种产出,m表示产出数量,s表示投入数量,n表示决策单元数量,ε表示非阿基米德无穷小量。利用该模型,能够对所有DEA决策单元进行排序[17-18]。