数学活动经验是指学习者在参与数学活动的过程中所形成的感性知识、情绪体验和应用意识.它是学生获得学科理解的催化剂和黏合剂,更是发展学生数学核心素养的助推器,是实现传统的知识教育向启迪学生智慧教育转变的有效途径.数学活动经验的获得、提升、迁移需要在“做”中获、“思”中提、“悟”中移. 数学实验是学生通过动手、动脑,以“做”为支架的教与学的活动方式,是在教师的引导下,学生运用有关工具,通过实际操作,在认知与非认知因素参与下进行的一种发现数学结论、理解数学知识、验证数学结论的数学活动.数学实验可以促进学生积累数学活动经验. 随机事件的概率是高中概率的核心概念,比较抽象,是学习的难点.下面,以本节课的教学为例,谈谈如何科学设计试验方案,帮助学生积累数学活动经验,发展数学核心素养. 一、教学内容分析 “随机事件及其概率”是人教A版《普通高中课程标准实验教科书·数学3(必修)》第三章“概率”的起始课,它既是之前统计知识的延续,也是古典概型、几何概型和概率分布的基础. 《普通高中数学课程标准(2017年版)》的要求是:结合实例,会用频率估计概率;加深对随机现象的认识和理解.因此,本节课的主要任务是了解随机事件发生的不确定性和频率的稳定性.并在此基础上抽象出概率的统计学定义.正确理解概率与频率的区别与联系,掌握用频率来估计概率的方法,进一步感受统计思维. 二、学情分析 学生在初中已经学过随机事件及其概率,对频率与概率的关系也有初步的了解.知道概率的描述性定义是“刻画一个事件可能性大小的一个确定的数”,知道“通过大量重复试验,可以用频率估计概率”.具备一定的用概率解释随机现象的经验.高中,刚刚结束了统计初步一章的学习.这为本节课的学习奠定了知识基础. 学生对频率稳定性的理解仅停留在感性认知上,对如何用数学工具准确刻画这种可能性,认知还比较模糊.高二学生已经具备一定的动手实践、合作探究的能力,思维能力也得到了较好的发展,为本节课的学习奠定了能力基础. 学生对非确定性现象的研究方法不太熟悉,缺乏相关的研究经验,需要教师加强指导. 三、教学目标 本节课的教学目标设置如下. (1)结合实例,进一步了解随机事件、必然事件和不可能事件的概念. (2)通过掷硬币试验,了解随机事件发生的不确定性和频率的稳定性;获得相应的操作性经验、合作交流的经验、数据分析的经验,发展数据分析素养. (3)理解概率的统计学定义,明确概率与频率之间的区别与联系,获得数学抽象的经验,发展数学抽象素养. 教学重点:了解随机事件发生的不确定性和频率的稳定性. 教学难点:理解频率与概率的关系. 四、教学策略分析 本节课的教学策略是:联系生活,激发兴趣;试验探究,合作交流;媒体应用,多元表征;抽象概括,应用升华. 五、教学过程设计 (一)创设情境 (1)联系生活,激发兴趣. 教师播放麦迪投3分球的视频,并给学生介绍这是2004年火箭队与马刺队的一场比赛.距离比赛结束还有35秒钟的时候,麦迪连续投中了3个三分球.将比分差距缩小至2分. 然后继续播放视频,在麦迪抛出第四个3分球的时候,教师按下暂停键,问:这个球能进吗? 播放视频,最后球进了,火箭队取得了胜利. (2)激疑问难,引发思考. 问题1:在麦迪抛出这个3分球之前,你知道他能否投中吗? 【设计意图】通过生活实例,让学生体会到学习随机事件的必要性. (3)温故知新,深化概念. 教师追问:“麦迪投3分球命中”是随机事件还是必然事件?什么是随机事件、必然事件、不可能事件呢? 教师让大家再列举生活中的随机事件、必然事件、不可能事件的一些实例. (4)逐步诱导,切入正题. 问题2:既然“麦迪投3分球命中”是随机事件,那么为什么队员把球送给麦迪而不是送给其他队员? 引导学生明确是因为麦迪投篮命中的可能性大. 教师追问:麦迪投3分球命中的可能性比其他队员命中的可能性大,这一生活经验是如何得到的? 学生思考:根据以往的数据,统计其投篮的命中率.投3分球的命中率=
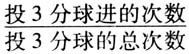
. (5)给出频率的定义. 在相同条件下进行n次重复试验,某一事件A出现的次数
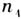
称为事件A发生的频数;称事件A出现的比例

为事件A发生的频率. 师:刚才的投篮命中率就是“投3分球命中”这个事件的频率.
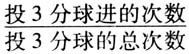 . (5)给出频率的定义. 在相同条件下进行n次重复试验,某一事件A出现的次数
. (5)给出频率的定义. 在相同条件下进行n次重复试验,某一事件A出现的次数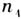 称为事件A发生的频数;称事件A出现的比例
称为事件A发生的频数;称事件A出现的比例 为事件A发生的频率. 师:刚才的投篮命中率就是“投3分球命中”这个事件的频率.
为事件A发生的频率. 师:刚才的投篮命中率就是“投3分球命中”这个事件的频率.