李昌官老师提出的“高中数学研究型教学”,让学生亲历知识发现、建构的过程,有助于学生更好地学会“用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界”.其ADE设计模型与“五环十步”教学模式,为高中数学教学设计提供了基本的思维框架.笔者使用它们指导了“计数原理”的教学设计,从实际情境入手,提出核心问题,指明研究方向;再通过学生已有的计数经验,寻求原理建构的方法;然后,顺势创设一些简单的计数情境,开启原理建构之旅.具体的教学设计如下: 一、前期分析准备 (一)学习内容分析 1.知识产生的背景与固着点分析. 数是数学的核心,数源于数(shǔ).生产生活中,经常会遇到大量繁杂的计数问题,并且,这些计数问题背后蕴藏着特定的规律.我们需要发现这些计数原理,并且运用它们简化计数问题.学生已经有数数和分类计数的生活经验,这些经验是计数原理产生的固着点. 2.知识生长的过程与阶段分析. 计数原理的形成历经了以下几个阶段:一是认识到生活中存在大量的计数问题,这些计数问题既繁杂又蕴含某种可简化计数的规律;二是从已有的计数经验和生活实例中归纳、抽象出一般性的计数原理;三是理解计数原理的核心是“分类”与“分步”;四是运用计数原理解决一些简单的计数问题. 3.知识建构的策略与方法分析. 计数原理是对生活实际中的相关现象进行分析、抽象并数学化的结果,它的主要建构策略与方法有四个:一是分解与转化,即将一个复杂的问题分解、转化为多个简单的问题;二是从特殊到一般,即从大量特殊的计数事实、经验与方法中抽象出一般性的计数原理;三是类比,即类比数的加法和乘法;四是分类、分步讨论,这是把复杂问题分解、转化为简单问题的具体策略与方法. 4.知识间的联系与结构分析. 计数原理是加法运算、乘法运算的延伸与推广,是生活中分类、分步背后所蕴含的数量关系的数学刻画.它与向量基本定理有异曲同工之处:都是通过分解、转化解决问题;都是把复杂的事情分解、转化为简单的事情后,先把简单的事情搞清楚,再解决复杂的问题.同时,计数原理是排列、组合、二项式定理等知识的基础. 5.知识的要点与本质分析. 计数原理的实质是通过分类、分步来达到以简驭繁的目的.其中分类、分步既是分解、转化的具体策略与方法,也是具有根本性、一般性的思考和解决问题的策略与方法.分类的关键是依据清楚、不重不漏;分步的关键是步骤清楚、相互独立、相互衔接、有效完成一件事. 6.知识的学科意义与教学价值分析. 组合数学不仅在基础数学中具有极其重要的作用,而且奠定了计算机革命的基础,而计数原理是组合数学的核心内容之一.分类、分步思想不仅是解决计数问题的基本思想和方法,也是解决很多其他问题的基本思想和方法.计数原理的建构过程是培养数学抽象、逻辑推理、数学建模和数学运算等数学核心素养以及数学研究能力的良好载体. (二)学生认知分析 1.学生认知基础分析. 学生已经有对简单问题的计数经验和能力,熟练掌握加法和乘法运算,也会用列举法和树状图解决一些简单的计数问题. 2.学生认知障碍及克服措施分析. 学生的一个认知障碍是计数原理的抽象过程,原因是不熟悉数学抽象的基本步骤和原则.对此,可以通过提问、追问等方式将抽象的过程逐步分解:第一步,思考如何分析计数问题的实例;第二步,小组合作讨论这类计数问题存在怎样的共同特征;第三步,思考如何去除这些问题的物理属性;第四步,运用数学语言表示. 学生的另一个认知障碍是对运用计数原理解决问题的本质理解.运用计数原理解决计数问题的关键在于“如何完成一件事”,而“如何完成这件事”的本质就是搞清楚“元素、位置、放置规则”.故而,可以在大量实例分析的过程中,有意识地利用框图解决问题. 二、教学目标设计 1.认识计数原理建构的背景与必要性,理解计数原理是刻画事物数量的数学模型. 2.通过对实际问题的分析,经历把实际问题抽象成数学问题的过程,提升数学抽象、逻辑推理、数学建模和数学运算等数学核心素养,体会其中蕴含的从特殊到一般、以简驭繁、类比、转化等数学思想方法. 3.通过计数原理在计数问题中的应用,深入理解计数原理的本质. 三、教学过程设计 (一)呈现背景,提出问题 背景1 截至目前,台州市城乡机动车总数已超过170万辆,今年平均每天新增300辆,成为近几年来我市新增机动车数量最多的一年.台州市机动车牌照形式为“浙J·■□□□□”,其中“浙J”为地区代码.如果现在要求“■”为大写英文字母T或Z,“□”为阿拉伯数字0~9之一,请想一想:按此方式编排,最多有多少个不同的牌照? 背景2 核糖核酸(RNA)分子由碱基按一定的顺序排列而成.已知碱基有4种,由成百上千个碱基组成的RNA分子的种数非常巨大.你知道它是怎么算出来的吗? 背景3
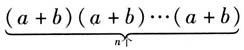
展开式有多少项?
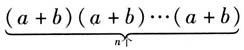 展开式有多少项?
展开式有多少项?