云南省图书馆机构用户,欢迎您!
02
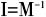 就可以确定X。
就可以确定X。 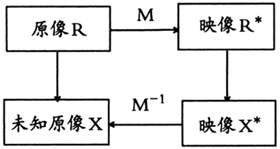 图1 RMI原则 复式记账测量记录的结构系统是指会计主体的全部经济业务,数学上称之为经济业务的集合S。对经济业务进行测量记录要借助于借贷记账法,经济业务与会计分录之间构成映射关系,会计分录的集合S*与经济业务的集合S形成了一一对应的关系。如果依据某种复式记账学说,在S*中执行了某种形式的数学处理,得出某些逻辑方面的结论X*;而且能从X*得到会计主体实证方面的某些结论X,则可以相信X的真实性。因为,在此测量过程中映射是一一对应的,反演也是一一对应的。用复式记账法测量得到的结果是会计分录集合S*,如果依据某个复式记账学说通过某种计算、运算等(准确地说是有限多步的数学处理)求出这一数量关系系统的某个(某些)性质X*,再通过反演(求逆映射)来确定经济关系系统中的对应性质X。复式记账的映射与反演关系如图2所示。
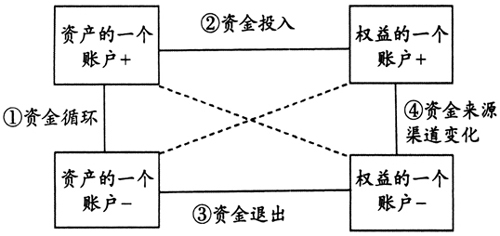
图1 RMI原则 复式记账测量记录的结构系统是指会计主体的全部经济业务,数学上称之为经济业务的集合S。对经济业务进行测量记录要借助于借贷记账法,经济业务与会计分录之间构成映射关系,会计分录的集合S*与经济业务的集合S形成了一一对应的关系。如果依据某种复式记账学说,在S*中执行了某种形式的数学处理,得出某些逻辑方面的结论X*;而且能从X*得到会计主体实证方面的某些结论X,则可以相信X的真实性。因为,在此测量过程中映射是一一对应的,反演也是一一对应的。用复式记账法测量得到的结果是会计分录集合S*,如果依据某个复式记账学说通过某种计算、运算等(准确地说是有限多步的数学处理)求出这一数量关系系统的某个(某些)性质X*,再通过反演(求逆映射)来确定经济关系系统中的对应性质X。复式记账的映射与反演关系如图2所示。 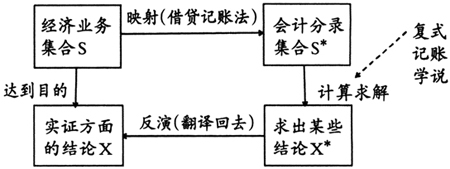 图2 复式记账RMI原则 对于会计主体这个经验系统,如果用观测或实验的结果做比对,结果相符,则说明反映和测量是成功的;若彼此常常相符,则可以认为复式记账很可能是正确的;若常常不相符,则可以认为复式记账法已被证伪,借贷复式记账法已被500多年的实践所证实。借贷复式记账法的“借”和“贷”归根结底是指增加和减少。因此,借贷复式记账法是对经济交易活动所做的“二元流体测量法”。 数学中对数学结构的定义是:在非空抽象集合上定义了适合一组公理的抽象关系,这个集合连同定义于其上的关系称为一个数学结构。可见集合理论与公理化方法是结构理论的两大支柱。基本的数学结构有三类,分别是代数结构、序结构和拓扑结构。在非空集合S上定义一个或几个二元运算,且运算满足一组公理,则称这个集合连同定义于其上的运算为一个代数结构,复式记账系统就是一种特殊的代数结构。 会计数据形成会计信息,复式记账系统是生产会计数据的系统,但至今人们对它的内部构造的认识还不清;由于复式记账系统是个数学系统,对它的数学结构认识不清,也就无法分析充分利用会计数据。只有运用恰当的数学工具,才能从庞大的会计数据资源中发掘出可靠的信息。复式记账所记录的内容是经济业务,它是指具有货币价值的交易或事项的转移、转变和转让等。经济业务是客观发生的,不以人的意志为转移。对于每一笔经济业务都要编写相应的会计分录,同样,记录的每一条会计分录都可以翻译成一笔经济业务。 要想弄清复式记账的本质,必须准确理解“复式”的真正意义。“复式”就是“二式”或“双重”的意思,主要包括两个方面:一是账户分为借、贷两方;二是每笔简单经济业务要记借、贷两笔账。在维持会计等式成立的前提下,全部经济业务只有四种类型(见图3):①资产的两个账户一增一减;②资产的一个账户与权益的一个账户同增;③资产的一个账户与权益的一个账户同减;④权益的两个账户一增一减。在复式记账中,根据经济业务之间的逻辑关系,将复式记账分为:分类复式记账(资产与权益)、因果复式记账(付现与收料、交货与收现)以及流程复式记账(位移、变换、组合和分解等)三种情形。
图2 复式记账RMI原则 对于会计主体这个经验系统,如果用观测或实验的结果做比对,结果相符,则说明反映和测量是成功的;若彼此常常相符,则可以认为复式记账很可能是正确的;若常常不相符,则可以认为复式记账法已被证伪,借贷复式记账法已被500多年的实践所证实。借贷复式记账法的“借”和“贷”归根结底是指增加和减少。因此,借贷复式记账法是对经济交易活动所做的“二元流体测量法”。 数学中对数学结构的定义是:在非空抽象集合上定义了适合一组公理的抽象关系,这个集合连同定义于其上的关系称为一个数学结构。可见集合理论与公理化方法是结构理论的两大支柱。基本的数学结构有三类,分别是代数结构、序结构和拓扑结构。在非空集合S上定义一个或几个二元运算,且运算满足一组公理,则称这个集合连同定义于其上的运算为一个代数结构,复式记账系统就是一种特殊的代数结构。 会计数据形成会计信息,复式记账系统是生产会计数据的系统,但至今人们对它的内部构造的认识还不清;由于复式记账系统是个数学系统,对它的数学结构认识不清,也就无法分析充分利用会计数据。只有运用恰当的数学工具,才能从庞大的会计数据资源中发掘出可靠的信息。复式记账所记录的内容是经济业务,它是指具有货币价值的交易或事项的转移、转变和转让等。经济业务是客观发生的,不以人的意志为转移。对于每一笔经济业务都要编写相应的会计分录,同样,记录的每一条会计分录都可以翻译成一笔经济业务。 要想弄清复式记账的本质,必须准确理解“复式”的真正意义。“复式”就是“二式”或“双重”的意思,主要包括两个方面:一是账户分为借、贷两方;二是每笔简单经济业务要记借、贷两笔账。在维持会计等式成立的前提下,全部经济业务只有四种类型(见图3):①资产的两个账户一增一减;②资产的一个账户与权益的一个账户同增;③资产的一个账户与权益的一个账户同减;④权益的两个账户一增一减。在复式记账中,根据经济业务之间的逻辑关系,将复式记账分为:分类复式记账(资产与权益)、因果复式记账(付现与收料、交货与收现)以及流程复式记账(位移、变换、组合和分解等)三种情形。