城市范围界定与标度律

      1 引言

      近些年，得益于智能手机和移动互联网的发展，城市研究领域可获得的微观数据越来越多；与此同时，城市研究学者从地理学、物理学、经济学等学科中借鉴了大量的模型思路和方法，促进了城市研究向着模型化、定量化、数据化方向发展[1]。但数据的增多让人容易陷入一个“误区”：轻信定量数据带来的结论，忽视了数据的产生过程与适用范围。数据的使用与待研究的问题密不可分，同一个研究问题，采用不同的数据可能得出相异的结论，即便使用相同的数据，但采用不同的处理方法，结果也可能大相径庭。这一点在近些年广受关注的城市标度律（scaling law）研究中尤为值得注意。

      标度律作为城市发展的重要规律之一，是指像道路网络、用地在内的城市属性在空间的自相似分布（在不同空间的时间尺度上重复一些模式），反映了城市内在的生长逻辑和集聚规律[2]。城市标度律的研究借鉴了许多其他领域的成果，像语言学中词频幂率分布的现象启发了对城市序位规模分布的探索[3-5]；而生物体新陈代谢率与个体尺寸的异速增长关系（allometric growth）则引导了对于城市异速增长的研究。生物领域的研究者发现，将不同物种的新陈代谢频率与生物体体积画到对数坐标上，每个哺乳动物几乎都落在一条斜率为3/4的直线上（这一规律通常被称为Kleiber law），这个关系式揭示了生物能量消耗的规模效应，质量越大的组织，单位质量单位时间的能耗更低[6]。这一规律最早由Naroll等[7]从生物学领域引入社会科学领域，后经由Nordbeck[8]、Lee[9]、陈彦光等[10-11]、Bettencourt等[12-13]多位学者从模型和实证的角度在城市研究领域将其发展完善，建立了更为系统的城市标度律分析框架。如果把人口N（t）作为时间t上城市规模的度量，城市标度律可以表示如下：

      

      式中：Y表示物质资源（例如基础设施数量）或者社会活动的度量（例如经济产出、污染量等）；N（t）代表t时刻的城市人口，用来衡量城市的规模；β作为指数反应了城市系统中的标度律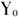；是一个标准化常量。根据β的大小，表征城市属性的变量可分为3组：①β＜1，是亚线性关系（sub-linear），通常是关于基础设施的参数，以人口增加导致的规模经济为特征。例如尽管纽约有4倍于休斯敦的人口，但纽约并不需要休斯敦4倍数量的加油站（加油站与人口的幂律指数为0.77）。②β≈1，是线性关系，通常和工作、住房、家庭用水量等个体需求相关，故与人口增加呈线性关系。③β＞1，是超线性关系（super-linear），通常城市的社会经济属性（也包括疾病、犯罪量等）属于此类，表明相应指标增长率要高于人口规模增长率，体现了城市的集聚效应。大量实证研究表明，标度律是城市组织的一种普遍性质，从横跨不同国家（美国、德国、瑞典、日本和中国等）的数据来看，都符合此规律[10-12]。图1a是2010年美国大都市统计区（Metropolitan Statistical Area，MSA）范围内人口数量和地区生产总值（Gross Regional Product，GRP）的双对数回归，图1b是人口与路网的双对数回归。这两组数据从数据的角度证明了经济随人口增长呈超线性关系，而路网呈亚线性关系（表1）。

      结合中国的数据，有许多关于城市标度律的实证研究。赖世刚等[14]分析了中国城市人口分布的位序—规模法则，指出1999—2009年中国城市人口分布的幂次现象日渐加强，城市趋于不均衡发展；李郇等[15]分析了1990年、2000年、2005年3年的中国城市用地与城镇人口之间的异速增长关系，认为1990年中国城市增长是负异速增长，2000年和2005年是正异速增长；陈彦光[16]认为异速生长与分形和自组织网络理论相互融合，并以河南为例，分析了城市人口和城市用地、城市产出等指标的标度关系，发现城市生长服从异速生长规律[10-11]。还有许多学者针对不同地区的数据进行了相似的分析[17-20]。

      

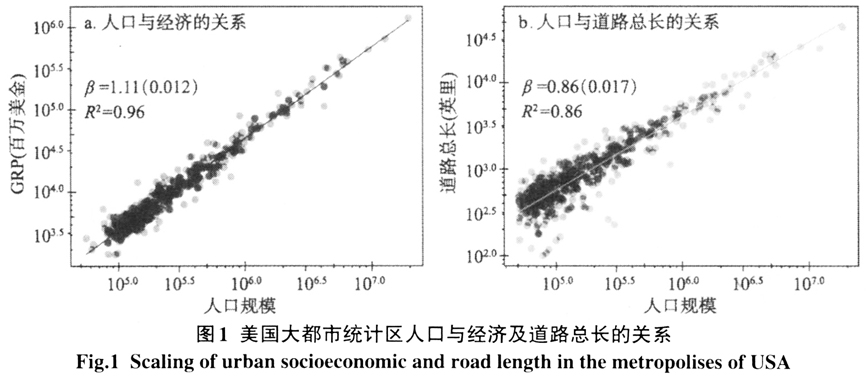      尽管这些研究都得到了相应的标度律系数，但使用的数据统计口径、回归模型各不相同，得到系数也有较大差别。究其原因，很重要的一点在于城市标度律的提出基于一个类比——城市可以类比成生物体。其中，城市的人口规模相当于生物体的质量，城市的经济活动相当于生物的新陈代谢。但城市与生物体的区别在于，城市并不存在一个清晰的边界，因此，如何找到合理的空间范围对应生物体的个体（body）就成了一个很重要的问题。特别地，城市边界选取的不同，分析结果可能迥异。例如在对于城市规模效应的讨论中，Gleaser等[21]认为大城市对环境更友好（体现在交通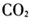排放量随人口数量的增长呈亚线性关系），而Louf等[22]通过分析数据发现，只是改变一下Gleaser等用的城市定义的边界，则会得出完全相反的结论。同样的数据集，如果在联合统计区（Combined Statistical Area，CSA）的尺度下分析，系数小于1，结论是大城市更节约能源，而如果用城市区域（Urbanized Area）当做分析单元，得出来的系数是1.37，结论反而是大城市不节能。随后又有一系列研究针对英国[23-24]、法国[25]的城市进行讨论，分析标度律的边界选取效应，发现边界选取对回归系数的影响很大。

      这些争议的出现促使作者思考，不同规律或者模型适用的空间尺度是什么？尤其是不同国家和地区的城市数据对应的空间范围各不相同，哪些数据和空间尺度更能反映城市标度律？标度律在不同国家又有什么异同？本文希望通过分析不同空间范围和数据源对应的标度律系数，并结合中美两国的对比研究，为此类问题提供新的视角。