2014年9月,国务院发布了中国物流业发展中长期规划(2014-2020年),明确提出将物流业作为国家基础战略性产业的地位。相比其他产业,物流业不仅仅是国民经济的重要构成,其发展水平还能够有效反映地区经济发展现代化和竞争力水平(Guo,2012)。经济新常态下,伴随“一带一路”国家战略的部署与实施,中西部地区对外开放的层次、范围将进一步提高,这有助于提升我国与“一带一路”沿线国家的战略合作水平,促进进出口贸易发展。进出口贸易的发展受物流业成本的直接影响(李保军,2013),而物流业发展水平则是决定物流成本高低的主要影响因素(赵艳玲,2005)。长期以来中国经济发展存在较明显的区域非均衡性,导致派生性的物流业发展也存在突出的区域非均衡矛盾。如果该问题长期内得不到有效解决,物流成本将伴随不同区域发展差距的扩大而不断高涨,从而降低我国出口商品的市场竞争力,对中西部地区与“一带一路”沿线国家经济协同发展产生逆向作用。鉴于此,本文从劳动力投入视角对我国物流业发展的非均衡性进行探讨。在时间维度下应用LMDI技术分解法对东中西部地区劳动投入总量从不同层面进行分解,将不同层面的结构变化对物流业产值总量变化的贡献进行量化分析;在空间维度下对物流业发展重心轨迹变化的影响因素进行研究。通过时间和空间双重维度探寻导致区域物流业非均衡发展的阶段特征及其内在影响因素,从而深层次挖掘导致非均衡发展的根源。 一、文献评述 相较生产性服务业中的金融业、批发零售业,有关物流业发展的内在影响因素研究较少。并且研究重点侧重于物流业发展的制约因素、外在影响因素、其他产业与物流业发展的关系等三个方面。其中,王微(2003)、罗峰(2007)、Muhammad和Saahar(2014)等国内外学者研究认为信息技术水平在物流业的应用程度较低是现阶段物流业发展的主要约束力量。并且Srinivas和Kollruru(2009)也证明信息技术创新能够提升物流业发展的竞争力。还有一些学者研究认为落后的基础设施是物流业发展的主要制约因素(李松庆,2002;Goh和Ling,2003)。此外,部分国内学者通过不同视角分析,研究结果均表明行政体制落后、缺乏有效的资金支撑以及高层次物流人才匮乏是现阶段物流业发展的主要制约因素(杜涛,2003;莫鸿等,2008;黄福华和刘长石,2009)。Dou等(2014)基于政策静态模型估计产业政策对物流业发展的影响,结果表明产业政策是物流业发展效率提高的主要制约因素。在物流业发展影响因素的研究中,Wang和Wang(2010)、姚娟和庄育良(2012)均认为中国不同地区FDI水平差异是物流业发展的重要影响因素。还有部分国内外学者以独特视角从区域资源禀赋差异、交通运输效率、低碳经济等视角进行研究(Liu,2013;Li和Shan,2014;Huang等,2014),结果表明不同视角所包含的因素对物流业发展均产生了较大影响。在其他产业与物流业发展的关系研究中,王珍珍和陈功玉(2010)从制造业劳动生产率视角研究,结论证明制造业劳动生产率提升对物流业发展具有较大影响。Zhang和Ju(2012)研究认为金融业发展的深度与广度对物流业发展具有较大影响。Yan(2014)研究发现物流业发展与工业结构具有前向和后向的相互影响。 从以上文献梳理可知,现有研究主要集中于对物流业发展的制约因素、外在影响因素的分析与探讨,缺乏对深层次的内在影响因素的研究。此外,现有文献还从产业层面研究了与物流业发展的关系,但是考虑到中国不同区域产业发展水平的差异,从产业层面并不能有效反映物流业发展的特征,从而也不能获知导致物流业发展非均衡性的内在根源,不利于国家和地区针对物流业制定专项的产业推进政策。通过对前人文献的梳理,本文基于现有研究进行了扩展:第一,应用δ收敛模型和β收敛模型对我国物流业非均衡发展的动态趋势进行定量化分析。第二,借鉴经济增长模型与C-D生产函数,将劳动力要素作为产业发展的内生影响因素,应用LMDI技术分解法和物理学重力模型原理,将劳动力投入进一步深入分解,从时间和空间双重维度探讨我国物流业非均衡发展的阶段特征及其成因。第三,构建能够实现物流业均衡发展的经济计量模型,通过实证研究分区域挖掘转变产业发展方式,实现均衡发展的有效路径。 二、物流业发展的非均衡性分析及假说提出 首先按照经济发展水平以及区位条件,我们将研究样本分为东中部、东西部和中西部三个经济区域,并对各地区所辖省份1998-2013年物流业劳动力投入规模、劳动效率和产值三个指标进行分类研究,分区域对非均衡发展的特征进行探讨。其次,在方法选择上应用δ收敛模型和β收敛模型对非均衡发展总体特征的动态趋势进行研究。其中,δ收敛模型计算方法如下:
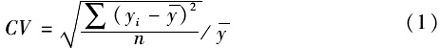
式(1)中,CV代表物流业发展的收敛系数;
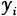
分别代表各地区的物流业产值、劳动投入规模、劳动效率。
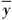
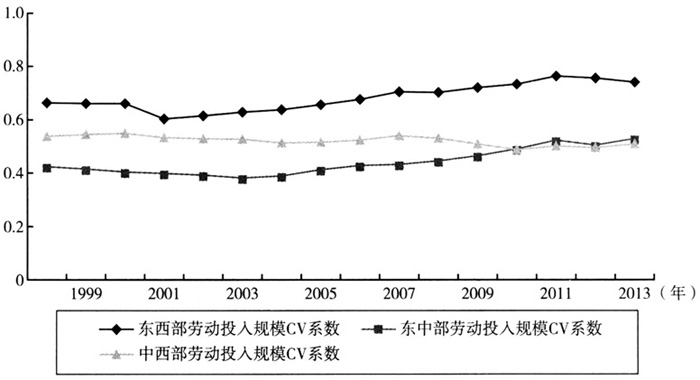
可代表各地区这一指标值的平均值;n代表经济区域所辖省份数量。通过对δ收敛模型进行数学计算得到CV收敛系数,如图1~图3所示。
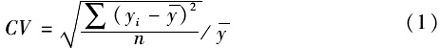 式(1)中,CV代表物流业发展的收敛系数;
式(1)中,CV代表物流业发展的收敛系数;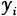 分别代表各地区的物流业产值、劳动投入规模、劳动效率。
分别代表各地区的物流业产值、劳动投入规模、劳动效率。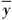 可代表各地区这一指标值的平均值;n代表经济区域所辖省份数量。通过对δ收敛模型进行数学计算得到CV收敛系数,如图1~图3所示。
可代表各地区这一指标值的平均值;n代表经济区域所辖省份数量。通过对δ收敛模型进行数学计算得到CV收敛系数,如图1~图3所示。 