1 概述 随着我国经济实力的不断提升、“一带一路”战略构想的纵深推进,以及长江经济圈、京津冀协同发展等区域经济布局的日益深化,物流产业在我国经济发展中的重要性逐渐显现,我国现代物流业开始步入发展的高峰时期。根据国家统计局2006-2014年《全国物流运行情况通报》披露的数据,我国社会物流总额由2006年的59.6万亿元攀升至2014年的213.5万亿元,物流产业效率也被纳入了考察一国经济运营效率的核心指标中。但是,我国物流基础设施存在明显短板,布局不合理、衔接不顺畅,综合交通运输体系、物流园区、物流技术装备等尚有很大的发展空间[1]。 在国内外学者已有的研究成果中,关于效率测算方法的研究有很多,农业、建筑业、金融业等很多行业早已对效率进行分析与评价[2-4],但长期以来,对于物流产业效率的研究仍相对不足。田刚等[5]选取1991-2007年间我国29个省物流业的面板数据,利用外生性影响因素和随机前沿生产函数模型进行联合估计,对我国物流业全要素的增长来源、差异与变化趋势进行实证分析。余泳泽等[6]选取随机前沿生产函数研究我国的物流产业效率,并探析物流资源利用率、地区制度变迁,以及区位优势等因素对我国物流产业效率的影响程度。张毅等[7]应用NEW-COST-DEA模型对17家上市物流公司2007-2009年间的成本效率进行测评,结果显示17家上市物流公司成本效率普遍较低。张中强[8]以我国东部31个地区的数据为样本,研究我国东部地区物流发展效率,并以2012年为典型年份,对区域物流发展的松弛变量及规模效率进行分析与评价。周会会[9]从物流业全要素能源效率指标分析出发,结合DEA应用原理构造中部6省全要素能源效率模型,并以中部6省原始数据为依托进行全要素能源效率拟合分析。学者们利用随机前沿生产函数、NEW-COST-DEA模型等方法对我国物流产业效率进行了一定的研究,但鲜有学者考虑到外部环境因素对物流产业效率的影响,因而容易造成测算结果的失真。三阶段DEA模型能较好的将外部环境因素纳入考量,从而得到更准确的结果。 长江三角洲地区目前已经成为我国经济飞速发展、经济总量最大、最具有发展潜力的区域。长江三角洲地区的物流基础设施较好,在加强铁路网、公路网、港航设施、航空枢纽等综合交通体系建设的同时,也正在大力发展现代航运服务体系。因此,利用三阶段DEA模型对江浙沪物流产业效率进行测算与评价,重点分析外部环境对江浙沪物流产业的影响,有利于定量分析长江三角洲地区物流产业发展现状,并为该地区物流产业发展提供参考。 2 研究方法与数据来源 2.1 三阶段DEA模型 FARRELL M J于1957年提出一种计量多种投入对农业生产效率影响的方法;CHARNES A等[10]于1978年在FARRELL M J研究的基础上得出了融合管理学、经济学及数学知识的DEA算法,扩充了生产函数的理论及应用范畴;FRIED H O等[11]于2002年研究得到三阶段DEA模型,其在测算生产效率时能有效地排除环境因素及随机误差,改进了传统DEA模型的不足。三阶段DEA模型包括以下3个部分。 2.1.1 第一阶段BCC模型 传统的DEA模型包括CCR模型和BCC模型2种,CCR模型假设规模效率不变,而BCC模型主要进行规模效率可变情况下的效率计算。BCC模型将综合效率(TE)分解成了纯技术效率(PTE)和规模效率(SE)的乘积,即TE=PTE×SE。 设有n个决策单元,每个决策单元都有m种类型的“输入”和s种类型的“输出”,则第
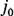
个决策单元总效率的计算就转化成线性规划问题,具有非阿基米德无穷小的DEA模型如公式(1)所示。

2.1.2 第二阶段SFA模型 在测算各决策单元效率时,第一阶段BCC模型得出的松弛变量是随机误差、外部环境和管理效率共同影响的结果。第二阶段SFA模型是在第一阶段DEA得到的松弛变量基础上,将投入松弛变量作为被解释变量,而外部环境及随机误差因素作为解释变量,建立SFA回归模型,排除外部环境及随机误差因素对投入松弛变量的影响,从而更加准确地反映管理无效率对决策单元效率的影响程度。 以投入导向为例,假设有n个决策单元,每个决策单元都有m种投入,有P个可测得的外部环境变量,分别对每个决策单元的投入松弛变量采用SFA分析,可得到SFA回归方程如公式(2)所示。

2.1.3 第三阶段调整后的DEA模型
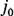 个决策单元总效率的计算就转化成线性规划问题,具有非阿基米德无穷小的DEA模型如公式(1)所示。
个决策单元总效率的计算就转化成线性规划问题,具有非阿基米德无穷小的DEA模型如公式(1)所示。  2.1.2 第二阶段SFA模型 在测算各决策单元效率时,第一阶段BCC模型得出的松弛变量是随机误差、外部环境和管理效率共同影响的结果。第二阶段SFA模型是在第一阶段DEA得到的松弛变量基础上,将投入松弛变量作为被解释变量,而外部环境及随机误差因素作为解释变量,建立SFA回归模型,排除外部环境及随机误差因素对投入松弛变量的影响,从而更加准确地反映管理无效率对决策单元效率的影响程度。 以投入导向为例,假设有n个决策单元,每个决策单元都有m种投入,有P个可测得的外部环境变量,分别对每个决策单元的投入松弛变量采用SFA分析,可得到SFA回归方程如公式(2)所示。
2.1.2 第二阶段SFA模型 在测算各决策单元效率时,第一阶段BCC模型得出的松弛变量是随机误差、外部环境和管理效率共同影响的结果。第二阶段SFA模型是在第一阶段DEA得到的松弛变量基础上,将投入松弛变量作为被解释变量,而外部环境及随机误差因素作为解释变量,建立SFA回归模型,排除外部环境及随机误差因素对投入松弛变量的影响,从而更加准确地反映管理无效率对决策单元效率的影响程度。 以投入导向为例,假设有n个决策单元,每个决策单元都有m种投入,有P个可测得的外部环境变量,分别对每个决策单元的投入松弛变量采用SFA分析,可得到SFA回归方程如公式(2)所示。  2.1.3 第三阶段调整后的DEA模型
2.1.3 第三阶段调整后的DEA模型