两步移动搜寻法及其扩展形式研究进展

      引用格式：陶卓霖，程杨.2016.两步移动搜寻法及其扩展形式研究进展[J].地理科学进展，35(5)：589-599.[Tao Z L,Cheng Y.2016.Researchprogress of the two-step floating catchment area method and extensions[J].Progress in Geography,35(5):589-599.].

      DOI：10.18306/dlkxjz.2016.05.006 修订日期：2016-04。

      1 引言

      公共服务设施对于满足人们日益增长的物质和文化生活需要及全面提升生活品质起着至关重要的作用。因此，公共服务设施的公平配置就成为其规划和布局的重要目标(Wang et al,2013；Dadashpooret al,2016)，尤其是在基本公共服务均等化的政策背景下，这一目标显得更为重要。空间可达性评价方法能够识别出公共服务的稀缺区域，是衡量公共服务设施布局空间公平性的有效途径(宋正娜等，2010；陶卓霖等，2015)，因此也受到国内外研究的广泛关注，并开发出了丰富的方法体系(宋正娜等，2010；Wang，2012)。其中，两步移动搜寻法(Two-step floating catchment area method,2SFCA)得到了广泛关注和应用，并且在后续研究中各种扩展形式层出不穷，形成了一个庞大的两步移动搜寻法模型族。在国内，近几年来两步移动搜寻法也受到越来越多的关注，在医疗(刘钊等，2007；胡瑞山等，2012，邓丽等，2015，付加森等，2015)、教育(任若菡等，2014)、养老(陶卓霖等，2014；赵东霞等，2014)、绿地(魏冶等，2014)、旅游景点(张鹏飞等，2015)等公共设施可达性以及就业可达性(王绮等，2015)等领域均有应用，并且对两步移动搜寻法的部分改进形式也有应用(任若菡等，2014；陶卓霖等，2014；魏冶等，2014；邓丽等，2015；张鹏飞等，2015)。但整体而言，国内研究中对两步移动搜寻法，尤其是其扩展形式的应用还较为有限。因此，本文通过对两步移动搜寻法的主要扩展形式进行系统梳理和总结，以期为相关研究的方法选择提供参考，促进两步移动搜寻法在国内相关领域的应用和发展。

      2 2SFCA的原始形式及与其他方法的比较

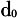      2SFCA最早是由Radke等(2000)提出，由Luo等(2003)进一步改进并命名为两步移动搜寻法。2SFCA的基本思想为：①对每个供给点j，搜索所有在j搜寻半径()范围内的需求点(k)，计算供需比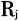；②对每个需求点i，搜索所有在i搜寻半径(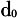)范围内的供给点(j)，将所有的供需比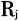加总得到i点的可达性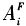(Luo et al,2003)：

      

      另一个较常用的可达性评价方法为重力模型法，也称为潜能模型(宋正娜等，2009)。实际上，2SFCA和重力模型法基于同一个理论框架(Luo etal,2003)，都综合考虑了设施的供给规模、需求规模和供需之间的距离关系对可达性的影响，两者的不同在于对距离因素的处理：重力模型法采用了连续型距离衰减函数，从而考虑了设施服务能力随距离衰减的特征，但并未对设施的有效搜寻半径进行限制；而2SFCA法采用二分法处理距离衰减，即在搜寻半径阈值范围内的可达性相同，而在搜寻半径范围之外则完全不可达。

      此外，还有其他几种较为常用的可达性评价方法：最近距离法只考虑距离因素，未对供需点规模因素进行考虑；Huff模型考虑了设施规模和距离因素，但未考虑需求点规模；核密度法实际上与重力模型法同属一个框架，采用的距离为欧氏距离，无法考虑实际交通网络的影响，也没有考虑需求点规模(陶卓霖等，2014)。

      综上可知，在众多空间可达性评价方法中，2SFCA和重力模型法应用最为广泛，考虑的因素最为全面，模型的理论基础相似，但2SFCA得益于两步移动搜寻的思想，易于理解，可操作性更强，因此得到了更多的关注和发展，为各种可能的扩展形式提供了可行的基本框架(McGrail et al,2009)。

      3 主要扩展形式

      3.1 基于引入距离衰减函数的扩展

      2SFCA原始形式中对距离衰减的处理为二分法。一部分扩展形式针对距离衰减函数进行扩展，本质上是在2SFCA的搜寻半径之内再加入一个额外的距离衰减函数，具体函数形式因扩展形式而不同。

      针对这类扩展，Wang(2012)提出了一个2SFCA的一般形式(Generalized 2SFCA)，在模型中加入一项距离衰减函数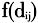，用于概括和表示不同扩展中的距离衰减函数形式：

      

      式中：f是一般化的距离衰减函数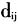；是i和j的距离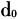；是搜寻半径，即设施的有效服务半径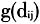；表示在搜寻半径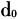范围内的距离衰减函数。在这一框架下，可将2SFCA的各个扩展形式对距离衰减函数的改进概括为对函数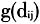的替代。2SFCA原始形式中将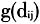处理为恒等于一个常数，而在扩展形式中，函数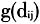可采用按距离区分权重的分段衰减形式、重力模型的距离衰减函数形式(如幂函数或指数函数等)、核密度形式或高斯形式等。下面介绍主要的几种距离衰减函数扩展形式(图1)。