0 引言 随着资源和环境问题日益严重,以资源再生利用、物料增值和成本节约为目的的逆向供应链(reverse supply chain)受到了社会各界的广泛关注。为此,许多学者从不同角度研究了逆向供应链决策问题[1-5],但不争的事实是,在分散决策下供应链上各主体的“自利”行为将产生双重边际效应(double marginalization),从而导致供应链效率损失[6,7],尤其是采用价格合同(price-only contracts)情形。尽管采用复杂的契约进行协调是减少供应链效率损失的重要途径[8,9],但这些复杂契约的实施具有较高的谈判成本和道德风险,而价格合同由于简单易用,且管理成本低,因而在实际运营管理中仍被广泛采用[10]。那么,能否确定出基于价格合同的供应链在分散决策下的效率损失上界,从而准确地衡量其双重边际效应呢? Koutsoupias和Papadimitriou[11]在研究由于用户的非合作行为而导致整个系统出现效率损失时,提出了非合作代价(price of anarchy,PoA)的概念。PoA问题的研究对非合作系统的效率分析和政策设计有重要价值,近年来已成为交通网络、网络资源分配、网络定价等领域的研究热点。Perakis和Roels[10]首次将PoA概念引入供应链领域,并将其定义为集中决策供应链与分散决策供应链在最差均衡下的收益比。在此基础上,研究了需求函数具有递增广义失效率(increasing generalized failure rate,IGFR)时,多种不同供应链结构下制造商和零售商基于价格合同进行分散决策时的效率损失。之后,Du等[12]考虑需求函数为已知区间上的任意随机分布但不具有IGFR性质,分析了推式供应链结构下的PoA值,结果表明价格合同在需求不确定性较低时可以保证供应链效率。刘天亮等[13]假设需求函数是凸的、需求弹性是关于销售价格的非减函数,基于PoA概念研究了分权供应链在运作效率和社会福利方面的损失问题。 对于两级的正向供应链,在销售价格固定、随机需求的情形下,双重边际效应导致供应链效率损失上界的极小值约为42%[10]。而在逆向供应链中,废旧产品在供应时间、数量、质量上的多重不确定性可能使问题变得更复杂[14]。然而,目前尚未发现针对逆向供应链中PoA的研究。人们不禁要问:逆向供应链只是正向供应链的简单逆过程吗?如何量化逆向供应链在分散决策下的效率损失?逆向供应链中双重边际效应的强度如何? 为此,本文在文献[10]的基础上,首次将PoA概念引入逆向供应链。针对采用价格合同的逆向供应链,考虑回收市场上废旧产品供应的不确定性,通过PoA值的计算分别确定了推式和拉式两种结构的两级和多级逆向供应链在分散决策时效率损失的上界,并通过数值分析对所得结论进行了验证,从而定量分析了双重边际效应对逆向供应链的影响程度。 1 问题描述 考虑图1所示由1个回收商和1个处理商组成的两级逆向供应链系统。设回收商以单位回收价格A向消费者回收某种废旧产品,并以价格w转给专业处理商进行处理。处理商的单位处理成本为c,处理后的再生产品每件售价为p。令r=p-c,表示再生利用单位废旧产品所产生的收益。

图1 逆向供应链系统 Fig.1 Reverse supply chain system 设市场上的废旧产品供应量为R,服从连续并严格递增的累积分布函数F(x),其概率密度函数为f(x),而
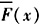
=1-F(x)为互补分布函数。假设分布函数具有IGFR性质(正态分布、均匀分布、指数分布、伽马分布、韦布尔分布、帕累托分布等许多分布都满足这一性质),以保证供应链博弈解的唯一性[10,15]。定义
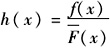
为失效率,g(x)=xh(x)为广义失效率。令
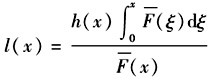
,当分布函数具有IGFR性质时,l(x)为递增函数[15]。 在正向供应链中,由于市场供需难以完全匹配,会引发产品库存积压或缺货风险[16]。而在逆向供应链中,同样存在供需不匹配的问题:由于在废旧产品供应量尚不明确之前就需要确定废旧产品的计划回收处理量Q,若Q大于市场上的废旧产品供应量R,将导致缺货风险;反之,则会出现回收处理计划不足,造成机会损失。在此假设废旧产品缺货成本为h,而机会损失不计。
 图1 逆向供应链系统 Fig.1 Reverse supply chain system 设市场上的废旧产品供应量为R,服从连续并严格递增的累积分布函数F(x),其概率密度函数为f(x),而
图1 逆向供应链系统 Fig.1 Reverse supply chain system 设市场上的废旧产品供应量为R,服从连续并严格递增的累积分布函数F(x),其概率密度函数为f(x),而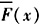 =1-F(x)为互补分布函数。假设分布函数具有IGFR性质(正态分布、均匀分布、指数分布、伽马分布、韦布尔分布、帕累托分布等许多分布都满足这一性质),以保证供应链博弈解的唯一性[10,15]。定义
=1-F(x)为互补分布函数。假设分布函数具有IGFR性质(正态分布、均匀分布、指数分布、伽马分布、韦布尔分布、帕累托分布等许多分布都满足这一性质),以保证供应链博弈解的唯一性[10,15]。定义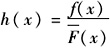 为失效率,g(x)=xh(x)为广义失效率。令
为失效率,g(x)=xh(x)为广义失效率。令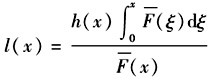 ,当分布函数具有IGFR性质时,l(x)为递增函数[15]。 在正向供应链中,由于市场供需难以完全匹配,会引发产品库存积压或缺货风险[16]。而在逆向供应链中,同样存在供需不匹配的问题:由于在废旧产品供应量尚不明确之前就需要确定废旧产品的计划回收处理量Q,若Q大于市场上的废旧产品供应量R,将导致缺货风险;反之,则会出现回收处理计划不足,造成机会损失。在此假设废旧产品缺货成本为h,而机会损失不计。
,当分布函数具有IGFR性质时,l(x)为递增函数[15]。 在正向供应链中,由于市场供需难以完全匹配,会引发产品库存积压或缺货风险[16]。而在逆向供应链中,同样存在供需不匹配的问题:由于在废旧产品供应量尚不明确之前就需要确定废旧产品的计划回收处理量Q,若Q大于市场上的废旧产品供应量R,将导致缺货风险;反之,则会出现回收处理计划不足,造成机会损失。在此假设废旧产品缺货成本为h,而机会损失不计。