doi：10.3969/j.issn.1674～4993.2015.11.041 【中图分类号】F253 【文献标识码】B 【文章编号】1674～4993(2015)11～0105～04 1 引言 在物流中心的各项活动中，分拣是最为重要的一项活动，其成本约是整个中心运营成本的50％～65％[1]，分拣的效率不仅关系到整个运营的成本还直接影响到客户服务水平。而订单分批通过将多个订单合成一个批次或更大的订单以提升拣选设备的利用率并减少工作量，使得分拣过程得以更有效地实施。随着订单数目的增加，可行批次的数量以及决策变量的数量呈指数增长，许多基于最优化算法的研究都具有比较大的局限性，所以采用启发式算法解决订单分批问题得到了广泛的共识。早期的研究主要凭借以往的经验对订单分批过程进行优化。例如对客户订单按照某种事先确定好的优先级进行分批，先到先服务(First Come First Serve，FCFS)准则是其中最常用的一种。Elsayed[2]在1981年提出种子算法的概念，该算法对每个批次选定一个种子订单，余下的订单将按照某种配对原则添加到批次中。Ho和Tseng[3，4]等对种子的选取规则以及订单配对原则的选取进行了深入的研究。李诗珍对种子算法以及节约算法进行了初步的探讨[5，6]。Elsayed和Unal[7]在节约算法的基础上提出了一种有效的算法用于求解订单分批问题，通过比较每两个客户订单合并后的路程节约量进行分批，从节约量最大的订单对开始，余下的订单对按照节约量非增的顺序被分配到下一批次中，每次分配订单的时候都重新计算节约量。 综上所述，订单分批问题的求解方法是国内外研究的重点，一些经典的启发式方法如先到先服务、种子算法、节约算法在实际中得到了广泛的应用，这些算法的特点是直观易行并且计算快速，常用来求得问题的初始解或作为检验新算法有效性的基准。本文提出一种降批次启发式方法，并与经典的算法进行比较。 2 问题描述和模型建立 订单拣选可以说是物流中心最耗费时间的作业，根据以往的经验，减少拣选所花费的时间能够有效节约人力成本。同时，拣选时间是交付提前期的重要组成部分，减少拣选作业时间能减少客户订货周期从而提升客户服务水平。 当客户订单到达，为了完成客户订单所指定的物品的拣选，拣货人员需要花费的时间也被称作订单处理时间，其中行走时间对整个订单处理时间的影响最大。假设拣货人员在拣货过程中采用匀速行走，减少行走时间可以等效为减少总的拣选路程。 订单分批是这样一个过程：待拣选的物品被安排到每一次往返于仓库的行走过程中，每次往返拣选一方面受限于拣选设备的容量，另一方面也取决于订单所包含品项占用的空间大小。客户订单尽量被安排到一次拣选路程中直到拣选设备的容量被用尽为止，这些需要在一次往返路程中完成的订单为一个批次。许多文献中拣选设备容量有不同的意义，既可以指订单的数目也可以是物品的数目，本文指的是物品的数目。综上，订单分批问题可以描述如下： 对于给定的拣选设备容量以及路径策略，如何将客户订单以及所要求的有固定储位的待拣选物品分批在一次往返拣选中完成从而使得所行走的路程最短? 本文采用Gademann和van de Velde[8]提出的订单分批模型，该模型具有简洁直观的特点非常适合用来进行订单分批问题的探讨，该模型明确考虑到每个可行的批次，设订单集合O有n个订单需要拣取，每个订单中含有一定数量的物品，并设B为可行的批次集合，可以建立如下数学优化模型： 目标函数：
该模型要求每批次订单在一次往返拣选路径中完成，以使得所有批次总的拣选路程最短。约束条件(2)保证了每批订单所包含的品项数不超过拣货设备的容量，约束条件(3)和(4)则保证了每个订单必须且只能被分配一次。 3 路径策略下的计算方法 上述优化模型的目标是最小化拣选路径，对于启发式算法的评估依赖于相应的路径策略，由于具体选择哪种路径策略并不会对评价分批结果的好坏产生影响，本文的算法采用S型路径策略。在实际应用中，S型路径策略是最为常见的，采用S型路径策略计算拣选路程不仅直观而且易于实现。本节讨论一种S型路径的计算方法，该方法灵活易于扩展，而且最为重要的是不影响我们对订单分批问题的讨论。一个典型的单区型无交叉走道的货架摆放如图1所示：
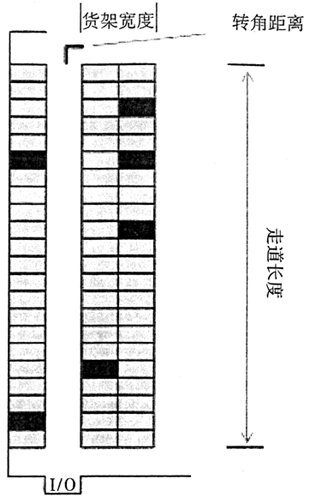
图1 仓库货架摆放示意图 则拣货人员在拣选过程中通过的路程可近似计算如下：D=LENGTH[，_OF_RACK]×(Nl+λ)+WIDTH×Nw+CORNER×Nc
