[中图分类号]F274 [文献标识码]A [文章编号]1000~1549(2015)11~0096~09 一、引言 经济学、营销学和运营管理领域的文献大多假设决策者完全理性,追求利润的最大化。实际上,管理者的社会倾向,如公平、利他等等,对企业的定价等决策和消费者购买决策具有重要的影响。[1][2]例如,为了在高通胀和货币贬值的市场能够促进供应链系统获得持续健康的增长,包括让瓶装厂得到足够的收益,可口可乐非洲区总裁Alexander B.Cummings决定提高已经维持了好几年的产品价格,即便提价的最大受益方不是自己,而是瓶装厂,这种利他的提价行为在六个月后引致供应链系统利润的共同提高。[3] 利他倾向广泛地存在于人们的日常生活中。[4][5]实证研究也发现博弈参与人具有利他倾向,人们的效用与他人的收益呈现一定的正相关。[6]国内的学者也有类似的发现。黄少安和韦倩(2008)[7]指出人们可以从利他行为中直接和间接获得效用。张同龙(2011)[8]分析调查数据后发现,企业的捐赠行为背后有利他动机在起作用。钟伟锋和徐宗玲(2006)[9]通过问卷调查发现决策主体并不是完全自利的,而是具有一定程度的利他倾向。由此可见,决策者往往不是完全理性,仅仅追求自身利润的最大化,而是会关心他人的利益,体现出一定的利他倾向。 本文即研究了利他倾向对供应链上下游企业的定价决策及均衡结果产生的影响。实际上,不考虑决策者利他倾向的供应链均衡决策问题已经受到了相当多文献的关注。McGuire和Staelin(1983)[10]、Coughlan(1985)[11]、Coughlan和Wernerfelt(1989)[12]探讨了供应商的渠道结构决策问题。Choi(1991)[13]探讨了三种具有不同讨价还价力量的分销渠道非合作博弈问题。Weng(1995)[14]研究了二层渠道下的数量折扣问题。Chu和Desai(1995)[15]、Desai(1997)[16]在需求不确定和异质性下研究了提高顾客满意和联接特许方和加盟方利益的协调机制。许明辉等(2006)[17]研究了二层供应链中Stackelberg和Nash博弈的参与方定价与服务决策。这些文献分别从渠道结构、权力结构、数量折扣等角度研究了二层供应链的博弈问题。但它们均是基于决策者“经济人”的假设,完全追求最大化的利润。 近年来,将决策者的社会倾向纳入到供应链均衡决策的分析,已经迅速成为供应链研究中的一个热点问题,特别是考虑公平偏好的供应链决策与协调问题,如Cui等(2007)[18]、Ozgun等(2010)[19]、杜少甫等(2010)[20]、杜少甫等(2013)[21]、李建斌等(2013)[22]、王磊等(2014)[23]。然而,相对于公平偏好,考虑利他偏好的供应链博弈研究还非常少见。目前仅有Loch和Wu(2008)[24]通过实验研究了利他偏好、自利偏好和竞争偏好三种情形下的供应链博弈问题。Ge Zehui(2012)[25]针对报童问题,考虑定价、订货量、广告,研究了生产商主导下的利他偏好对供应链批发价契约和效率的影响。与之不同的是,本文在三种渠道权力结构[13]下分析了利他偏好对供应链成员的均衡决策和最优战略的影响,深入探讨了利他倾向、渠道权力对供应链成员定价、利润和效用的作用机制。并据此提出了管理启示。期望为供应链管理的研究提供一个新的视角。 二、假设与模型 考虑由一个生产商和一个零售商组成的典型的二层分销渠道,前者生产一种产品以获得最大化的利润,后者以批发价从前者购买这种产品,并出售给市场中的消费者以最大化自身的利润。市场需求量依赖零售价格且为线性关系,具体形式是q=a-bp,其中,a是严格正的参数,表示该产品的市场潜在规模,b是顾客需求对零售价的敏感度。假设生产商生产出恰好满足市场需求的数量。上述信息均为公共知识。这样,生产商和零售商的利润函数分别如下:
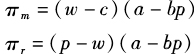
当生产商和零售商均具有利他偏好时,双方的决策目标不再是上述的利润函数,而是追求最大化自身的效用。为此,采用加权求和形式将利他偏好引入双方的效用函数[24][25],具体形式如下:

δ、ξ分别表示生产商、零售商的利他偏好系数,且二者属于[0,1],这是符合常理的假设。正常情况下,人们对自己利润的关心程度要高于对别人的关心程度。δ、ξ的取值越高,意味着双方利他之心更强。当二者均为零时,即退化为不考虑利他偏好的问题。也就是说,本研究是对已有文献的推广。本文考虑三种渠道权力结构,即生产商Stackelberg、零售商Stackelberg和纵向纳什,分别简记为MS、RS和VN。[13]博弈规则、求解顺序参见该文献。由于推导过程并不复杂,为节省篇幅在此省略,博弈均衡结果直接在表1给出。
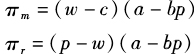 当生产商和零售商均具有利他偏好时,双方的决策目标不再是上述的利润函数,而是追求最大化自身的效用。为此,采用加权求和形式将利他偏好引入双方的效用函数[24][25],具体形式如下:
当生产商和零售商均具有利他偏好时,双方的决策目标不再是上述的利润函数,而是追求最大化自身的效用。为此,采用加权求和形式将利他偏好引入双方的效用函数[24][25],具体形式如下:  δ、ξ分别表示生产商、零售商的利他偏好系数,且二者属于[0,1],这是符合常理的假设。正常情况下,人们对自己利润的关心程度要高于对别人的关心程度。δ、ξ的取值越高,意味着双方利他之心更强。当二者均为零时,即退化为不考虑利他偏好的问题。也就是说,本研究是对已有文献的推广。本文考虑三种渠道权力结构,即生产商Stackelberg、零售商Stackelberg和纵向纳什,分别简记为MS、RS和VN。[13]博弈规则、求解顺序参见该文献。由于推导过程并不复杂,为节省篇幅在此省略,博弈均衡结果直接在表1给出。
δ、ξ分别表示生产商、零售商的利他偏好系数,且二者属于[0,1],这是符合常理的假设。正常情况下,人们对自己利润的关心程度要高于对别人的关心程度。δ、ξ的取值越高,意味着双方利他之心更强。当二者均为零时,即退化为不考虑利他偏好的问题。也就是说,本研究是对已有文献的推广。本文考虑三种渠道权力结构,即生产商Stackelberg、零售商Stackelberg和纵向纳什,分别简记为MS、RS和VN。[13]博弈规则、求解顺序参见该文献。由于推导过程并不复杂,为节省篇幅在此省略,博弈均衡结果直接在表1给出。