基于神经网络组合模型的物联网产业发展预测研究

      一 引言

      物联网产业发展战略规划和相关政策的制定，要求对物联网的发展前景进行科学、准确的定量研究。但由于物联网产业发展时间短、历史数据少，缺乏统一的官方统计数据，并且物联网产业涉及领域广、数据收集难，在此方面的研究需要适应性更强、准确度更高的方法。①李遵白，杨德林(2011)等人用两种方法对物联网市场进行了预测：一种是以电信业和RFID产业作为自变量，通过构建物联网产业的关联方程来预测物联网产业的产值；另一种是采取问卷调查的形式，调查物联网领域的学者和相关从业人员对物联网产值的预测。两种方法都具有合理性，但研究方法较为粗糙，主观性和随机性较强，结果准确度较低。黄迪(2011)利用灰色预测模型，构建GM模型对RFID市场规模数据进行分析，但该模型只是单纯地通过对时间序列分析来了解系统的运动规律，并没有对系统的结构机理进行探讨，在处理复杂的非线性关系时准确度较低。人工神经网络的自适应性强，能够利用函数增加样本数量，调整网络结构以适应物联网产业发展的规律，以最优的方式预测物联网产值，弥补物联网数据不足、误差较大的缺点，可以有效地提高预测的准确性，但单个网络模型容易陷入局部收敛，达不到全局最优。因此本文在两个单个神经网络检测的基础上，建立了BP-RBF组合神经网络来预测物联网产值。

      二 模型构建及样本处理

      1.BP、RBF神经网络及组合预测模型

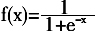      BP神经网络由多层构成，所使用的传递函数一般是Sigmoid函数，定义为：。本文采用动量梯度下降算法(TRAINGDM)来训练网络，该方法是对BP法的改进，通过增加动量因子α，能够稳定学习率，使网络具备了一定的抗震动能力和加快收敛的能力，适合于数据少、误差大的物联网产业的预测。

      RBF神经网络的隐含层是非线性的，将输入向量空间转换到隐含层空间，使原来线性不可分的问题变得线性可分。径向基函数一般为高斯函数，其表达式为：

      

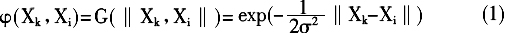      式中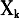，为第k个输入训练样本，k=1，2，…，P，P为样本数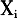；为第i个高斯函数的中心，i=1，2，…，N，N为隐含层点数。本文采用newrbe函数创建一个严格的径向基函数，该函数适用于物联网数据样本较少的情况，能够建立一个误差几乎为零的神经网络。Spread表示径向基函数的扩散速度，在训练网络时，可通过不断调整来达到理想的效果。

      组合预测模型是由Bates和Granger(简称BG)在1969年第一次提出。如果将单项预测看作不同信息片段，那么组合模型可以通过信息的集成，来分散单项预测的不确定性，提高预测精度。我们在组合预测时仍采用RBF网络模型，在单个预测结果的基础上，进行模拟训练，对比三种训练结果并进行最终预测。

      2.确定训练及检验样本

      《物联网“十二五”发展规划》将物联网产业划分为感知制造业、通信业和应用服务业。感知制造业主要包括RFID、传感器、智能仪器仪表等前端产品的制造，②这些起到基础和支撑作用产业，其产量在很大程度上决定了物联网产业的规模；通信业是实现物联网物物相连、人物相连的媒介；处在产业链下游的服务业包括云计算、物联网软件与设备销售服务业和物联网应用服务业，是物联网发展的最终目标。此外，投资规模的大小不仅决定了该产业的发展规模和方向，还体现了这一产业是否具有投资价值和发展潜力，因此，也对物联网产业规模产生巨大的影响。

      为保证数据的准确性，本文中RFID、传感器、仪器仪表产量构成的制造业数据来自于中国仪器仪表行业协会、中国传感器网和中国物联网；云计算、软件销售、应用服务业等数据来自于2006-2012年《中国统计年鉴》和中国物联网；投资规模来自于中国物联网。对于缺失的数据，本文采用指数平滑、取均值等统计方法进行了处理。

      本文选取2005-2011年物联网产业数据，其中将2005-2009年的历史统计数据作为BP和RBF网络模型的训练样本，2010和2011年的历史统计数据作为BP和RBF网络模型的检测数据，并对2012-2020年的物联网产值进行了精确预测。

      3.样本归一化处理

      本文采用均值法，即用每个指标数据比上该项指标数据的平均值，来对数据进行归一化处理。该方法可以在消除量纲和数量级影响的同时，保留各变量取值差异程度上的信息，也就保留了指标的可比性，差异程度越大的变量对综合分析的影响也越大(韩胜娟，2008)。

      归一化公式：

      式中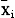为该项指标的平均值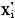，为第i个指标的无量纲化指标值。归一化之后的数据见表1。