文章编号:1002-3100(2014)11-0001-04 近年来,地震、泥石流、旱涝等自然灾害的频频发生,造成了巨大的人员伤亡和财产损失。在目前的科技水平下,这些自然灾害事件是不可避免的,所造成的损失也是无法估量的[1-2]。因此自然灾害发生时,科学合理的资源配置能对应急救援起到事半功倍的作用,然而应急物流配送车辆调度优化就是其中的关键环节,越来越多的人认识到应急物流配送车辆调度优化问题的重要性。 应急物流与普通物流相比,有很多相同的地方,不过也存在很多不同的地方,节约成本是普通物流主要考虑的因素,然而应急物流配送过程中要受到严格的时间约束,因此应急物流更体现了应急服务的时效性。目前国内外对应急物流系统的研究主要有应急车辆的配置、应急资源调配和应急配送车辆调度,在应急物流配送车辆调度模型以及算法上都有了一定的研究,Eqi等人建立以运输成本最小为目标的调度模型[3],宋远清等在研究了需求随机的车辆调度模型,但是没有考虑运输成本和运输时间[4];石玉峰等建立了最短运输时间和最小运输费用的多目标组合优化调度模型[5];文仁强等通过蚁群算法对应急物资配送车辆调度优化问题进行了求解[6];张裕华等在带有时间窗的基础上考虑运输费用与距离构建应急物流配送车辆调度模型,并运用了蚁群算法进行求解[7];陈明华建立了一般性非满载应急物流车辆调度模型,采用人工免疫算法进行了求解[8]。综上所述,在车辆调度问题中多注重时间方面的及时性,忽略了应急运输车辆的体积和载重对配送调度的影响以及应急配送车辆资源的有限性,通过本文的研究,建立更符合实际的多目标应急配送车辆调度优化模型,运用针对该模型的混合算法求解模型得到的结果可以作为救灾指挥中心制定车辆调配方案科学决策的依据。因此,本文所研究的问题具有重要的现实意义。 1 模型构建 1.1 模型的问题假设 (1)所有受灾点在物资数量方面和运输时间方面的需求都能够得到满足,同时单个需求节点的需求量小于单车最大荷载;(2)同种车型运输,车辆的额定载重量和车辆的容积一定;(3)各受灾点均在救灾点的配送范围之内,运输到受灾点的时间不超过最迟到达时间;(4)路网为完全网络,即所有节点之间都有线路连通;(5)救灾点与各受灾点、各受灾点之间的运输距离作为已知量;(6)每辆车完成配送任务后回到配送中心。 1.2 模型的数学描述 有n个受灾地区向救灾指挥中心请求救灾物资的配送,第i个受灾节点对于救灾物资的需求量为
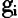
(i≠0),救灾中心与各受灾节点、各受灾节点之间的广义运输距离为
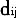
,运输时间为
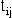
(i,j=0,1,2,…,n,配送中心编号为0,受灾节点编号为1,2,…,n);卸货时间为

,最迟允许车辆到达时间为
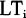
;G是一系列需要应急服务的受灾点集合;K表示应急运输车辆集合;
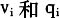
,分别表示受灾点i应急物资的体积和重量;V和Q分别表示运输车辆额定体积载重;可用车辆数为k;车辆不能超载且必须在规定时间之前把物资送到受灾节点。要求指派运输车辆,并确定每辆车运输路线,使得总运输距离最低,并且使运输车辆最少。 把应急配送中心即救灾点和受灾节点统一看做是运输网络中的节点。设在同一线路上点i是点j前面的相邻点,车辆到达点i的时间为
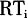
,到达j点的时间为
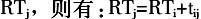
。 将模型中所涉及的二进制变量定义如下:

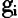 (i≠0),救灾中心与各受灾节点、各受灾节点之间的广义运输距离为
(i≠0),救灾中心与各受灾节点、各受灾节点之间的广义运输距离为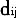 ,运输时间为
,运输时间为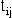 (i,j=0,1,2,…,n,配送中心编号为0,受灾节点编号为1,2,…,n);卸货时间为
(i,j=0,1,2,…,n,配送中心编号为0,受灾节点编号为1,2,…,n);卸货时间为 ,最迟允许车辆到达时间为
,最迟允许车辆到达时间为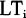 ;G是一系列需要应急服务的受灾点集合;K表示应急运输车辆集合;
;G是一系列需要应急服务的受灾点集合;K表示应急运输车辆集合;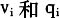 ,分别表示受灾点i应急物资的体积和重量;V和Q分别表示运输车辆额定体积载重;可用车辆数为k;车辆不能超载且必须在规定时间之前把物资送到受灾节点。要求指派运输车辆,并确定每辆车运输路线,使得总运输距离最低,并且使运输车辆最少。 把应急配送中心即救灾点和受灾节点统一看做是运输网络中的节点。设在同一线路上点i是点j前面的相邻点,车辆到达点i的时间为
,分别表示受灾点i应急物资的体积和重量;V和Q分别表示运输车辆额定体积载重;可用车辆数为k;车辆不能超载且必须在规定时间之前把物资送到受灾节点。要求指派运输车辆,并确定每辆车运输路线,使得总运输距离最低,并且使运输车辆最少。 把应急配送中心即救灾点和受灾节点统一看做是运输网络中的节点。设在同一线路上点i是点j前面的相邻点,车辆到达点i的时间为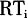 ,到达j点的时间为
,到达j点的时间为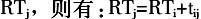 。 将模型中所涉及的二进制变量定义如下:
。 将模型中所涉及的二进制变量定义如下: 