景区建设对区域经济发展的响应格局演变

       中图分类号：F592.7 文献标志码：A 文章编号：1000－3037(2014)06－0956－11

       区域差异发展是现代经济发展的一种常态，把握区域发展差异有利于区域均衡发展，旅游作为国民经济发展的一个重要组成部分，对国民经济发展具有举足轻重的作用。旅游发展依赖于景区发展，因而景区空间格局研究已成为旅游研究的重要方面。目前，研究集中在目的地演化模式、景区空间分布特征、目的地－客源地空间关系三个方面。在演化模式研究方面，学者试图运用区位论[1]、核心边缘[2-3]、点轴[4]、中心地理论[5-6]等经典的区域空间结构理论来解释旅游地空间结构的演进规律，并运用这些理论来指导旅游开发。在空间分布特征方面，学者运用紧密度指数、最邻近点指数、地理集中度指数、分形指数等数理统计方法[7-8]和Voronoi图、密度分析、空间自相关、可达性等空间分析方法[9-12]，对A级景区、世界遗产等不同类型旅游景区在多个空间尺度上进行了广泛的研究，探讨了景区格局的区域差异[13]及其景区的经济影响域[14]等。在目的地－客源地空间关系研究方面，学者主要从旅游供给与旅游需求的地域分布规律和空间联系特征出发[15]，探寻景区的市场域及其各级阈值[16-17]；近年来，学者还从旅游目的地间空间位移[18]、旅游路线选择[19-20]等视角建立计量模型来研究目的地－客源地空间关系的演化特征。

       以往景区空间格局研究主要侧重于空间布局研究，而对景区建设和其他相关要素之间的关系及其作用机理缺乏深入的探讨，区域经济发展无疑是影响旅游景区建设至关重要的要素之一。那么在考虑区域经济变化的基础上，区域旅游景区的变化呈现出什么样的格局，格局的影响因素和作用机制又如何？这都亟待深入的探讨研究。此外，上述景区空间差异的研究大多假设区域之间相互独立，不存在任何相互作用。而事实上，区域发展的相关理论和实践表明，区域之间存在着扩散(涓滴)或极化(回波)效应，可以缩小或扩大区域空间差异[21]，传统的区域经济差异度量方法，因其缺乏空间视角，忽略了空间的影响，尤其是空间相关性和异质性。基于此，本文构建旅游景区格局对区域经济发展的响应指数，以江苏省为例，运用空间变差函数，深入分析区域旅游景区建设和区域经济发展的内在关系、空间格局、演变过程和影响因素，为区域旅游健康发展提供理论指导。

       1 研究区域与分析方法

       1.1 研究区域及其旅游景区的选择

       江苏省既是旅游资源的高富集区，又是主要的客源产生地，旅游经济高度发达。从需求看，该地区2012年人均GDP突破10000美元，旅游需求将向高品质、个性化的旅游方向发展；从供给看，该地区旅游景区建设步伐明显加快，旅游景区密度已高达4.87个/，高密度成为江苏省景区分布的基本特征。因此，分析江苏省旅游景区空间分布对区域经济发展的响应差异更具理论意义和应用价值。

       中国国家旅游局在1999年颁布了《旅游区(点)质量等级的划分与评定》标准。自该评定标准颁布以来，已经深刻而显著地改变了我国旅游景区(点)建设和管理长期落后的面貌，因而本文以A级旅游景区作为研究对象，选取2001、2005、2009和2012年4个年份以及2001—2005、2005—2009、2009—2012年3个时间段作为研究断面，选取68县域单元为研究对象，数据资料取自《江苏省统计年鉴》。对行政区划调整的区域进行相应的合并处理，以保持数据的连续性。

       1.2 分析方法

       1.2.1 响应指数

       借助于弧弹性公式来构建响应指数模型：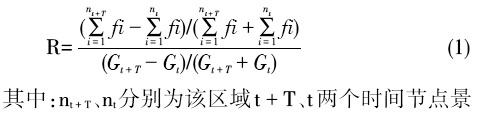

      

      

       1.2.2 空间变差函数

      

       其中：N(h)是分隔距离为h的样本量。空间变差函数是在区域化变量满足平稳条件和本征假设的条件下定义的。数学上可以证明，半变异函数大时，空间自相关减弱。距离是方差图的最重要特征，此外，方向也是一个重要的特征量，即各向同性和各向异性。以h为横坐标，以γ(h)为纵坐标，可以绘制出空间变差函数的曲线图，如图1所示。从图中可以直观地看出区域化变量的空间变异性。图中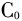称为块金方差，表示区域化变量小于观测尺度时的非连续性变异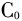；＋C为基台值，表示半变异函数变量随着间距增加到一定尺度后出现的平稳值；C为结构方差；a为变程(半变异函数达到基台值时的间距)。在变异理论中把变程a视为空间相关的最大间距，也称为极限值。另外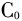值的大小反映了变化的幅度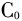，→0反映连续变化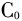，越大变化幅度越大，块金系数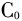/(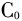＋C)，反映这种变化程度。表征变差函数的第4个参数是分维数，其数值由变异函数γ(h)和间隔距离h之间的关系来确定：