将实际问题转化为线性规划

      在现实生活中，我们常常需要制定效益或效果最好的工作方案。例如，制衣厂的原材料确定，在预测几种服装的销售情况下，如何安排生产，可使制衣厂总利润达到最大？钢板厂的任务一定，如何安排剪裁方案，使耗用的钢板最少？采油厂的油井情况已确定，如何安排生产，使总成本达到最低？

      有一些问题中的量，可以用多元一次函数，即线性函数来表示（或近似表示）。因此，一大类实际问题，可以转化为线性规划问题。我们看几个例题便可了解。

      例1 煤矿甲每年产煤4万吨，煤矿乙每年产煤7万吨。城市A 每年耗煤3万吨，城市B每年耗煤8万吨。 已知从各个煤矿到各个城市的每吨煤的运价如表1。

      表1 原煤运价表（元/吨）

      

      在上述条件下，应如何制定调运方案，才能使总运费达到最小？将这个问题转化为线性规划模型。

      解 假设从煤矿甲运到A城为x[,11]吨，运到B城为x[,12]吨；从煤矿乙运到A城为x[,21]吨，运到B城为x[,22]吨。此处x[,12]的右侧下角标12中，第一个数字1代表第1行，第2个数字2代表第2列，其余类推。我们注意到总产量等于总销量，就可列出下面的产销平衡表（表2）。

      表2 产销平衡表（单位：万吨）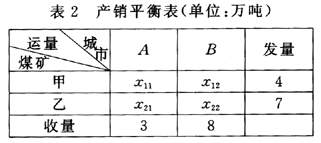

      

      表2的最右边一列，注明了从甲矿运出了4万吨，从乙矿运出了7 万吨。表2的最下面一行，注明了A城收到了3万吨，B城收到了8万吨。 按照产销平衡条件，我们有

      x[,11]

       ＋x[,12]

      

      

      

      

      

      

      

       ＝4（甲产煤量）

      

      

      

      

      

      

      

       x[,21]

      

      ＋x[,22] ＝7（乙产煤量）

      x[,11]

      ＋x[,21]

      

      

      

      

      

      

      

       ＝3（A耗煤量）

      

      

      

      

      x[,12]

      

      

       ＋x[,22]

      

       ＝8（B耗煤量）

      满足上述四个等式的未知数x[,11]，x[,12]，x[,21]和x[,22]的一组非负值，便是我们的一个运输方案。因此，我们称x[,11]，x[,12]，x[,21]，x[,22]为决策变量。

      总运费是多少？我们记总运费为f，就有

      f＝20x[,11]＋50x[,12]＋30x[,21]＋70x[,22]

      我们的问题，就是找决策变量x[,11]，x[,12]，x[,21]，x[,22]的一组值，既满足上述四个等式，又满足非负值条件，并且还要使总运费目标函数的值达到最小值。总运费称为目标函数。

      这里要提醒读者的是，满足上述四个等式及非负值条件的决策变量的值有无限多组，每一组值对应于一个总运费，因此，求总运费的最小值这一问题是有意义的。现在，我们将上面的叙述紧缩为线性规划模型：

      minf

       （最小化f）

      f＝20x[,11]＋50x[,12]＋30x[,21]＋70x[,22]

      （目标函数）

      

      说明 在上述模型中，x[,11]，x[,12]，x[,21]，x[,22]叫做模型的决策变量。符号“minf”，读作“求f的最小值”或“最小化f”。符号s.t是英文“subjectto”的缩写，读作“受约束于”。四个等式总称为主约束，四个不等式总称为非负约束。等式和不等式，总称为线性规划的约束条件，而f称为线性规划的目标函数。

      题1 假设有A、B两煤矿、每月产煤分别为23万吨和27万吨。它们生产的煤分别供应发电厂甲、乙、丙，每月需煤量分别为17万吨，18万吨，15万吨。从A矿到甲、乙、丙三厂的每吨煤的运价分别为50元，60元，70元；从B矿到甲、乙、丙三厂的每吨煤的运价分别为60元，90元、110元。寻求使总运费达到最小的运输方案。

      请读者自己将这一问题转化为线性规划模型。

      例2 某农户承包土地100亩，现在每年的种植方式有三种（对每一块土地而言，每年只能采取其中的一种）：一季小麦，一季水稻；一季油菜，一季水稻；一季绿肥，一季水稻。有关的效益系数和技术系数预测如表3：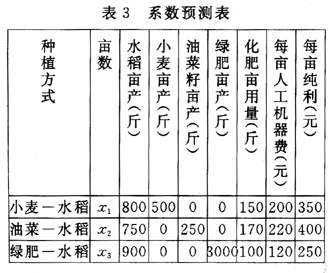

      

      该农户从自己的条件出发，要求种植计划（即x[,1]，x[,2]，x[,3]的一组非负值）满足下列各项要求：

      第1，水稻产量不少于8万斤；第2，小麦产量不少于1万5千斤；第3，油菜籽产量不少于1万斤；第4，绿肥产量不少于10万斤；第5，化肥使用量不超过1万4千斤；第6，人工机器费用不超过2万元。