任意角的三角函数的教学设计与说明

      一、教材分析

      （一）教学内容

      

      （二）地位和作用

      任意角的三角函数是三角学内容的基础，是后继内容学习的思维起点，是整个三角学认知结构的.它的学习既是学科系统内部知识发展的需要，又是坐标思想、数形结合思想、运动变化观念渗透的载体，更是对函数概念理解和认识的一次升华.学习过程中的认知冲突，不同思维的碰撞，易激发学生思维的积极性，有助于探索、创新能力的培养.由锐角三角函数的定义到任意角三角函数的定义是学生认识上的一次突破和飞跃，也是体悟特殊与一般辩证思维的良好素材.

      二、学情分析

      学生在初中学过的锐角三角函数是以锐角为自变量，相应边的比值为因变量的函数，这是学生学习任意角的三角函数知识的基础和依据，但学生必须面临由特殊到一般的认知过程，必须经历由直角三角形对应边的比值到直角坐标系中坐标与距离比值的转换.当学生在原有认知结构中具备同化新概念的适当观念，具备有意义学习的心向后，更容易激发学生学习的热情，催生创造性思维.当新概念产生后，如何用函数的观念认识理解新概念，把新概念纳入到一般函数的结构之中，既是认识过程中的一道坎，又是认知的一次升华.

      三、教学目标

      （一）知识与技能

      掌握任意角的三角函数的定义，会判断任意角的三角函数的符号，在形成定义的过程中领悟坐标法的优越性，加深对函数概念的理解.

      （二）过程与方法

      引进坐标思想，建立（x，y）与（r，a）之间的关系；通过联想锐角三角函数的定义，思考如何定义任意角的三角函数；理解锐角三角函数是任意角三角函数的特例；通过对比值符号的确定，培养学生掌握、利用规律解决问题的意识.

      （三）情感态度、价值观

      培养学生在运动变化的过程中认识知识的发生和发展，体会知识之间的内在联系，感悟知识的整体性.通过合作交流，培养主动探究新知识的能力.

      四、重点、难点

      （一）重点

      1.对任意角的三角函数定义的理解；

      2.正弦、余弦、正切函数值在各个象限内符号的确定.

      （二）难点

      用一般函数的概念理解任意角三角函数的定义.

      五、教法、教具

      （一）教法

      本课采用“引导—探究式”教学方法，将问题以问题串的形式展现，让学生在愤悱中形成认知冲突，体会、感悟数学研究的一般思路和方法.

      （二）教具

      投影仪，多媒体课件.

      六、教学过程

      （一）概念的引入

      问题1 在初中，我们已经学习过锐角三角函数的定义，请回忆在Rt△OMP（∠M=90°）中（如图1）：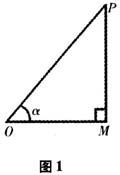

      

      sinα=____，cosα=____，tanα=____，它们是以什么量作为自变量，什么量作为因变量的？

      问题2 引入弧度制以后，自变量α在什么范围内变化？sinα，cosα，tanα是两条线段的比值，这些比值在什么范围内变化？

      设计意图：以锐角三角函数的定义为起点，以高中函数定义的三要素为依托，将锐角三角函数融入学生已有的函数知识结构中，容易为学生建立起任意角的三角函数获取心理逻辑的自然.

      问题3 锐角三角函数的定义域是锐角，当∠α变为钝角时，“∠α的对边，邻边”这些说法还存在吗？此时∠α的三角函数又该如何定义呢？

      设计意图：利用∠α的变化作为思维的切入点，打破学生已有的认知结构的平衡，感受学习新知识的必要性——角的范围扩大了，锐角三角函数的定义也应该与时俱进，这有利于将探究的主动权交给学生.

      （二）概念的形成

      问题4 我们曾研究过多种函数的性质，请回忆：在研究函数的性质时，通常是借助什么工具来实现的？

      设计意图：依托学生已有的经验，启发学生联想，触发学生的灵感，形成用坐标法解决问题的心向.

      问题5 如果让你把图1中的直角∠OMP放置于直角坐标系中（或利用图1建立直角坐标系），怎样放置比较合适？

      设计意图：数学实验是数学学习所必需的.或许不同的学生会有不同的方法，但对通过点P的坐标表示的讨论，可以让学生在选优的过程中达成共识（如图2）.