车辆路径问题优化　　

      国家发展改革委、国家统计局、中国物流与采购联合会2013年2月26日公布的“2012年中国物流运行情况通报”显示[1]，2012年全国社会物流总费用约为9.4万亿元，同比增长11.4%，约占GDP的18%，几乎相当于欧美水平的2倍。其中，运输费用高达5.3万亿元，约占社会物流总费用的56.38%。面对高昂的物流成本，如何通过优化运输过程中的车辆路径来降低运输费用从而最终达到降低物流成本的目标是物流研究中的一个热点问题。

      车辆路径问题(Vehicle Routing Problem，VRP)可以描述为[2]：已知某一配送中心，有一批具有足够数量且有载重限制的配送车辆和一组有确定需求量的客户，在满足一定的约束条件下(如车辆载重约束、客户时间窗约束、配送完成返回配送中心约束等)，按照各个客户的需求合理规划车辆的行车路线，从而达到一定的目标(如耗费时间最少、配送距离最短、使用车辆最少、花费配送成本最少等)。车辆路径问题最早是由Dantzig和Ramser[3](1959年)提出的，经过五十几年的发展，关于车辆路径问题的求解算法经历了从刚开始的精确算法(又称最优化算法)，到后来的传统启发式算法，再到现在的现代启发式算法的发展历程。精确算法能求得较小规模VRP问题的最优解，但是随着问题的复杂化，计算量呈指数增长；遗传算法[4]、蚁群算法[5]、粒子群算法[6]等现代启发式算法能求得较大规模VRP问题的满意解，但普遍存在算法复杂、收敛慢、执行时间较长等缺陷；而传统启发式算法中的节约算法由于其应用简单、易于理解并能有效平衡算法复杂度和问题复杂度之间的关系受到企业管理者的青睐。但是节约算法经过多年的实践检验，发现该算法存在装载率低[7]和配送路径交叉的缺陷[8]，本文结合分割配送和扫描法对传统节约算法进行改进，以期这一问题能得到改善。

      1.传统节约算法

      1.1 传统节约算法原理

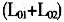      1964年，Clarke和Wright提出了C-W节约算法，解决了一般性的以最短路为优化目标的车辆路径优化问题。其基本原理如下[9]：已知某配送中心给两个客户送货，完成配送任务后车辆需返回配送中心，并且两客户的需求之和不超过车辆载重。若配送中心派两辆车单独给两客户进行配送(如图1所示)，车辆的行驶距离为L=2；若配送中心将这两个客户并入到同一条配送路径中，用同一辆车进行配送(如图2所示)，则车辆的行驶距离为L=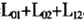。根据三角形两边之和大于第三边的性质，可知图2的配送方案比图1的配送方案节约的里程为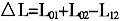。显然并入到同一条路径中的客户越多，节约的里程越大。例如，将某一客户并入到图2所示的配送路径中(如图3)，已知三个客户的需求之和不超过车辆载重，此时节约的里程为。

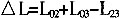      按照这种思路，当配送中心给多个客户送货时，可以将各个客户按照节约里程量的大小依次并入到配送路径中，若并入某客户后，该路径上的货物总量超过了车辆的载重，则剔除该客户，同时该配送路径规划结束。余下的客户用同样的方法确定配送路径，直至所有的客户都被安排到配送路径中。

      

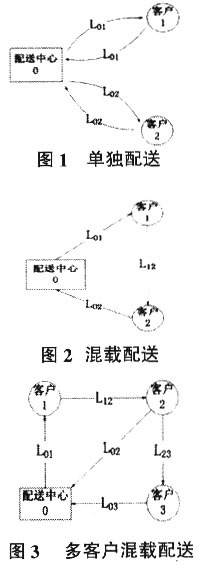      图1 单独配送

      1.2 传统节约算法计算实例

      某配送中心(编号为0)有N辆配送车辆(载重均为2吨)，现给10个客户进行送货，已知配送中心及客户的坐标位置及需求量(如表1所示)，求解最优配送路径。

      

      利用节约算法求解最优配送路径的步骤：首先根据表1中给出的配送中心及客户的坐标，利用欧式距离公式计算出配送中心及客户间的欧式距离；再通过节约法计算连接任意两个客户的节约里程，并按从大到小的顺序排列，得到节约里程顺序表；最后遍历节约里程顺序表，并根据是否超出车辆载重来判断是否应该将相应的客户并入配送路径中，若没有超载，将该客户并入配送路径中；否则不并入，同时该配送路径规划结束，启用下一辆车进行配送。求得配送路线为：

      

      利用谷歌地球软件确定配送中心与客户的相对位置，根据节约算法求解出的结果画出配送路径图(如图4)。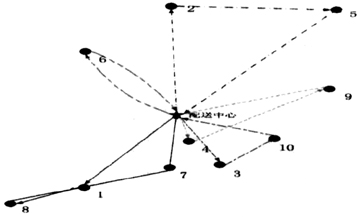

      

      图4 传统节约算法配送路径图

      1.3 传统节约算法的缺陷分析

      根据上述的实例计算可以发现，传统节约算法存在两个严重的缺陷。

      首先，传统节约算法不允许客户的货物分批配送，即每一个客户的需求必须一次性完成配送。其进行路径规划的判断依据是连接后该路径上货运总量是否超过配送车辆的载重，在规划配送路径的过程中，如果连接任何一个客户都会使车辆超载，则结束该条配送路径的规划，并启用下一辆车进行配送，这样可能导致某些路径的车辆并未满载，从而导致车辆的整体装载率偏低。从上述案例规划的配送路线可以看出，5条配送路线的装载率分别为90%、75%、80%、80%、60%。结果总的装载率仅为77%。由于每发动一辆车需要花费的固定成本包括人员和车辆的机会成本、年检费、保险费、车船税等一系列费用，远比配送过程中所花费的运输成本高得多，因此，提高车辆的装载率，即尽可能使用最少的车辆完成所有客户的配送任务可以有效地降低配送成本。