高级科学人才集聚成长的时空格局演化及其驱动机制　　

      修订日期：2013-02.

      1 引言

      当今世界竞争的关键是人才的竞争(Beechler et al，2009；王辉耀，2010)，核心是高级人才的竞争(刘少雪，2009)。在国际竞争日益激烈的大背景下，中国结合新世纪、新阶段的发展任务和时代挑战，明确提出了人才强国的基本战略(李燕萍，2010)，也进一步提出要突出培养领军式高级人才，为加快转变经济发展方式、实现科学发展提供人才保证(白春礼，2007)。科学的高级人才实践发展呼唤科学的高级人才理论指导。高级人才现象具有空间属性(叶忠海，2000)，基于地理学视角对高级人才群体进行分析，可以剖析出其不同成长阶段过程中的时空分布和迁移规律、扩散、演化格局及其影响机制，地理学理应成为研究高级人才群体发展和变化的重要学科。

      目前，国内外地理学界对高级人才研究主要集中在对高级人才空间静态或动态分布进行描述并对其成因、开发和规划进行定性简析等视角。例如，Marc(2009)分析了影响英国高级人才空间分布差异的成因及其结果；谷人旭等(2001)分析了上海市高级人才资源开发及其优化管理问题；刘超等(2004)对中国科学院院士的成材因素进行了初步研究；姜怀宇等(2005)分析了20世纪90年代以来中国人才分布的空间变动态势及其成因；任泉香等(2007)分析了近现代中国杰出女性人才的空间分异；罗守贵等(2009)分析了高级人才空间流动因素；李双双等(2011)对中国当代地理教授、研究员时空格局进行了分析；张建伟等(2011)研究了江苏省科技人才的空间差异及其演变态势。从空间集聚视角对高级人才成长的时空规律及其演化机制进行系统研究则较少(吴殿廷等，2006)。

      因此，本文以中国科学院院士为典型群体，运用空间计量方法识别和剖析高级科学人才成长的时空规律及其演化机制，从宏观层面为中国及其各省区市制定适宜的高级科学人才发展战略提供理论指导，也为国内外其他类型高级人才成长和发展研究提供一定的理论与方法借鉴。

      2 样本来源与研究方法

      2.1 样本来源

      不同职业及其级别差异使高级人才类型也有所不同。本文主要从学术地位及其贡献角度界定高级人才，即指在主要科学技术领域已取得系统性、创造性成就的学者总称(吴殿廷等，2003)；以中国科学院院士和中国工程院院士为典型代表；其中，中国科学院院士为高级科学人才的最高代表。中国科学院院士(以下简称中科院院士)，原称“中国科学院学部委员”，1993年10月改为现名，是中国大陆最优秀的科学精英和学术权威，每2年增选1次。1955-2011年间共产生14批中科院院士(含已故院士474人，不含外籍院士)，总人数为1192名。

      本文以此为典型样本进行分析，能对识别高级科学人才和其他类型高级人才成长和发展的时空规律有所启示。

      2.2 研究方法

      以省域为地域尺度，利用上述样本数据分析籍贯或出生地①、国内最高学历(位)获取地②和长期工作地③等中科院院士成长过程中3个重要阶段所在地的时空分布差异，选取4个不同年代④重点剖析中科院院士在上述3个重要阶段所在地的空间集中化和均衡度以及时空集聚演化格局及其特征。借助Matlab软件和GeoDa空间计量软件对相关数据进行处理、计算和可视化分析。

      2.2.1 基尼系数和集中化指数

      为了分析4个不同年代中科院院士在籍贯或出生地、国内最高学历(位)获取地和长期工作地的不同省域空间集聚情况，本文通过计算不同成长阶段的基尼系数来定量分析中科院院士在不同省域的集聚态势。基尼系数的计算方法如下(吴殿廷，2004)：

      

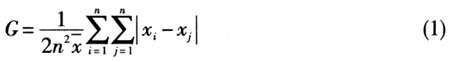      式中：G是基尼系数；n代表省域总数；x代表变量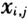的均值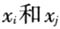；分别为3个重要阶段任意2个省域的中科院院士密度⑤。可以看出，G的值在0～1之间，系数越高，表明集聚值越大，即中科院院士在地理空间上的集聚程度越高；即当他们完全在空间上均匀分布时G值为0，完全集中在一起时G值为1。

      在一定程度上可以说，基尼系数的测度反映了中科院院士成长过程中3个重要阶段所在地的空间分布集聚化态势，但这一态势是否客观和真实，需要同样在数学上与基尼系数有等价关系的集中化指数来反映空间分布集聚化态势。集中化指数的计算方法如下(林炳耀，1985)：

      

      式中：I是集中化指数；A为不同省域中科院院士密度的累计百分比(由大到小)总和；R为中科院院士密度均匀分布时的累计百分比总和；M为中科院院士密度集中分布时的累计百分比总和。可以看出，I值也在0～1之间，指数越高，表明集聚值越大，即中科院院士在地理空间上的集聚程度越高；即当他们完全在空间上均匀分布时I值为0，完全集中在一起时I值为1。