修订日期:2012-02-18 中图分类号:K901 文献标识码:A 文章编号:1000-0690(2012)06-0649-09 交通事故是现代社会威胁人身安全和造成经济损失的重要因素,随着中国近年来机动车数量的急速增长,城市交通事故的数量也随之不断上升,因此如何减少交通事故的发生成为城市研究关注的话题之一。为了提出交通事故的预防措施和制定有效的交通管理制度,理解交通事故发生的原因、时空间分布特征等方面是至关重要的内容。 城市交通事故研究是国内外研究的热点主题之一,研究的重点包括两类,其一是对交通事故研究方法的研究探讨,尤其是空间分析方法,其二是和对交通事故影响因素的研究。交通事故数据通常是具有社会经济属性的空间点事件,目前国内外学界已有大量点事件的空间分析方法,包括样方分析、最近临近距离、核心密度估算、K函数等[1~5]。对交通事故影响因素的研究包括行人、机动车、道路状况、自然环境和人文因素等方面,其中被提及的因素从多到少依次是个人行为、机动车行驶速度和路面状况等[6~10]。诸多研究中隐含了不同的尺度,如交通个体的微观尺度、特定路段的中观尺度和整个城市的宏观尺度,其中城市的宏观尺度最能够说明城市交通事故的总体特征,理解整个城市的交通事故时空间分布特征是归纳事故影响因素的关键。 针对城市交通事故的时空间分布特征学界有着大量的研究,主要关注于时间分布特征和空间分布特征两方面。在时间分布特征上,一般认为城市交通事故在白天高于夜间、下午高于上午、出行高峰时段多于非高峰时段[11],弱势群体死亡事故多发生在夜间[12],并且在交通流量高峰时段,交通事故与交通流量呈正相关关系[13]。在空间分布特征上,有学者认为城市道路交通事故高发点多集中在城乡结合部位的出入口道路上[14],也有学者针对城市边缘区进行研究发现愈接近城区事故愈多,愈远离城区事故愈少[11],且普遍同意交通干线的事故高于交通支线。但是,上述研究仅分别对时间和空间分布进行研究,鲜有二者相结合的真正意义上的交通事故时空间特征研究,且对空间的关注要重于时间,时间只是相关要素中的其中一个。因此,本文将重点研究城市交通事故的时空间关系和特征。 学界普遍接受的观点是,城市交通事故的时间分布特征是交通事故高峰会出现在交通流量高峰时段,即交通事故数量与交通流量成正相关关系。如Kingham等[15]在对新西兰克里斯特彻奇市2000~2004年的交通事故研究中显示,交通事故高峰出现在8∶00,15∶00和17∶00,这3个时间段分别为早上班高峰,下午放学高峰和晚下班高峰。这种“常识性”的认识是交通事故时间分布特征未被重视的原因之一。但有研究发现了一个与普遍观点相反的结论,即交通事故的高峰并没有出现在上下班的交通高峰时段内,而是稍晚于上下班高峰时段,即出现在交通由拥挤到消散的时期(交通消散期)。造成这种现象的原因包括交通消散期内驾驶员谨慎程度放松、情绪烦躁、出行匆忙等方面[14]。该解释从个人行为的角度进行分析,但并未结合事故高发时段的空间特征以及相关的空间因素进行研究,且以主观的描述为主,实证支持不足。 针对城市交通事故高峰出现在交通消散期这一现象尚未有更多的研究,在西方依赖于高速公路通勤交通的背景下,交通事故数量确实与交通流量正相关[16,17]。但受众多因素的影响的城市交通是开放的系统,与封闭的高速公路事故情况不同。国内学者也少有进一步的研究。因此本文以惠州市惠城区中心城区为例,首先验证城市交通消散期内交通事故高峰现象是否存在,其次以城市交通消散期事故的特征为切入点,置于整个城市交通事故的时空间过程之中,总结交通消散期事故高峰的时空间特征,最后分析交通消散期事故高峰现象的形成原因。 1 数据与方法 1.1 数据 本研究选择惠州市中心城区作为研究区域。惠州位于广东省东南部,珠江三角洲东北端,是惠州市中心城区是惠州市,交通事故集中发生的区域。 交通事故和路网数据来源于惠州市公安局,选取2010年的50823条交通事故记录,按5%抽样率等距抽取2541条数据,经过自动地址匹配得到交通事故的有效空间数据1972条,其中位于中心城区的数据有1469条,再经过人工校核排除错误信息,最终确定1143条空间点数据。这些数据包括事故发生地点、发生日期、发生时间、严重程度和碰撞车辆类型等属性。路网数据包括了公路、主干道、次干道和支路的9659条多段线。 1.2 研究方法 本文采用核心密度估算(Kernel Density Estimation)对交通事故进行分析,该方法的优势在于便于研究事故危险的扩散性,即某一确定事故群的周围可看做事故的潜在发生地。核心密度估算可以在二维的地理空间内生成空间点事件的光滑密度表面,其一般形式是:
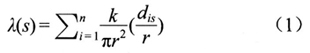
其中λ(s)是位置S的密度,r是核心密度估算的搜索半径(只有r范围内的点才进行核心密度估算),k是点i到位置S距离
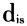
的权重,k通常是
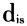
与r比值的函数(kernel函数)。核心密度估算采用一种能实现距离衰减效果的模型函数,即点i到位置 S的距离越远点的密度值就越低。最终,位置S在半径r范围内的所有点的密度值加和为位置S的密度。目前有多种形式的函数可以应用于以“距离衰减”为基础的空间权重的计算,通常选择kernel函数的一种,即Gaussian函数[18]:
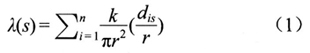 其中λ(s)是位置S的密度,r是核心密度估算的搜索半径(只有r范围内的点才进行核心密度估算),k是点i到位置S距离
其中λ(s)是位置S的密度,r是核心密度估算的搜索半径(只有r范围内的点才进行核心密度估算),k是点i到位置S距离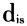 的权重,k通常是
的权重,k通常是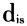 与r比值的函数(kernel函数)。核心密度估算采用一种能实现距离衰减效果的模型函数,即点i到位置 S的距离越远点的密度值就越低。最终,位置S在半径r范围内的所有点的密度值加和为位置S的密度。目前有多种形式的函数可以应用于以“距离衰减”为基础的空间权重的计算,通常选择kernel函数的一种,即Gaussian函数[18]:
与r比值的函数(kernel函数)。核心密度估算采用一种能实现距离衰减效果的模型函数,即点i到位置 S的距离越远点的密度值就越低。最终,位置S在半径r范围内的所有点的密度值加和为位置S的密度。目前有多种形式的函数可以应用于以“距离衰减”为基础的空间权重的计算,通常选择kernel函数的一种,即Gaussian函数[18]: