修订日期:2012-04-11 中图分类号:F512.99 文献标识码:A 文章编号:1003-2398(2012)06-0076-05 1 引言 通达性的概念是由Hansen[1]首先提出,将其定义为交通网络中各节点相互作用机会的大小,也称为可达性、易达性。通达性是目前国际交通运输地理的研究热点之一[2],如日本学者Murayama曾研究了1868-1990年间日本铁路发展对日本城市通达性的影响[3],欧洲学者Javier G曾对欧洲铁路网络的通达性变化进行了评价[4]。国内对于通达性的研究起步于1980年代末,到目前为止,国内的学者对交通网络通达性的研究呈现出多尺度、多方法和多时间段的研究特征[5]。多尺度主要体现在国家尺度[6-8]、区域尺度[9-11]和城市尺度的研究[12-14];多方法主要体现在可达性[15]、分形理论[16]、复杂网络理论[17]、空间句法[18]、拓扑理论[19]、最短路径[20]等;多时段主要体现在不同时间尺度上区域交通网络通达性的演变等,如李红对2000-2009年间中原城市群高速公路通达性及空间格局变化进行了研究[21]。综上,交通网络的研究无论从研究方法上还是研究尺度上均取得了一定的研究成果,但从研究尺度上看,大多数研究主要集中在国家尺度和城市内部两个主要的层面上,对于中尺度城乡交通网络通达性的研究相对较少;其次从研究方法上看,对交通网络的研究主要采用一种方法从单一的角度对交通网络进行定量评价,从而使得评价结论具有一定的片面性。 城乡交通网络是城乡社会、经济发展的命脉,是促进区域经济发展的先决条件[22]。城乡综合体系的演化与交通网络的发展是一种空间互动过程,交通运输网络是形成城乡体系网络系统的物质条件和必要前提[23],交通网络的通达程度决定了城乡各地理单元空间相互作用的广度和深度,交通网络的发展是改变经济活动区位优势的重要因素之一[24]。城乡交通网络的通达程度反映了区域运输能力及其与外界交流联系的便利性,从区域交通网络通达性方面揭示区域交通网络地理空间特征成为当前研究的焦点。我国城乡经济社会统筹发展的步伐不断加快,促进城乡联系更加紧密,而作为城乡联系的命脉—交通网络则面临着严峻的考验,解决的关键是对现有的交通网络进行优化和合理的规划道路建设。鉴于此,本文以徐州市城乡交通网络为例,基于交通网络分形理论、通达性理论对徐州市交通网络的空间形态、空间分布,拓扑关系、时间关系等进行多角度的分析,以期为徐州市城乡交通网络优化布局提供理论依据。 2 研究方法与数据来源 2.1 研究方法 利用交通网络分形理论和通达性理论,引入长度—半径维数模型、分枝维数模型、距离、时间可达性模型、可达性系数等模型,从空间形态、空间分布,拓扑关系、时间关系等角度研究徐州市城乡交通网络的通达性特征。 2.1.1 交通网络分形模型 (1)长度—半径维数模型 长度—半径维数反映了交通网络分布密度从测算中心向周边区域的变化情况。长度—半径维数是在交通网络长度L(r)与研究区域半径r之间存在幂指数函数关系的基础上经计算获得的[9,10],其测算方法如下: 对于任一几何体,其长度为L,面积为S,体积为V,M为广义体积,D为欧氏维数则有如下关系:

如果一个面积为S的区域内交通网络具有分形特征,则根据式(1),交通网络的总长L(S)与区域面积之间应有以下关系:
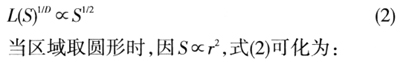

(2)交通网络分枝维数模型 交通网络的连通情况和复杂程度由交通网络分枝数变化率所确定的分枝维数来表达。分枝维数的计算方法与长度—半径维数类似。设半径为r的区域范围内,交通网络的分枝数为N(r)则由下式定义:

交通道路网的分枝维数反映交通网络的联通情况和空间结构的复杂性,如果分枝维数越高,说明城市交通网络越复杂,城市道路网的连通性就越高,单位面积内路网的数量就高;反之,城市交通网络越简单,城市交通网络的连通性就越低,单位面积内路网的数量就越低。 2.1.2 通达性模型 (1)距离可达性,即一个给定的节点到其他各节点最短距离之和。此距离越短,表示该节点的可达性越好。式(6)中
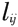
表示节点i到节点j的最短距离,则节点i的距离可达性定义为:
 如果一个面积为S的区域内交通网络具有分形特征,则根据式(1),交通网络的总长L(S)与区域面积之间应有以下关系:
如果一个面积为S的区域内交通网络具有分形特征,则根据式(1),交通网络的总长L(S)与区域面积之间应有以下关系: 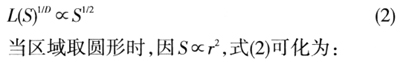
 (2)交通网络分枝维数模型 交通网络的连通情况和复杂程度由交通网络分枝数变化率所确定的分枝维数来表达。分枝维数的计算方法与长度—半径维数类似。设半径为r的区域范围内,交通网络的分枝数为N(r)则由下式定义:
(2)交通网络分枝维数模型 交通网络的连通情况和复杂程度由交通网络分枝数变化率所确定的分枝维数来表达。分枝维数的计算方法与长度—半径维数类似。设半径为r的区域范围内,交通网络的分枝数为N(r)则由下式定义:  交通道路网的分枝维数反映交通网络的联通情况和空间结构的复杂性,如果分枝维数越高,说明城市交通网络越复杂,城市道路网的连通性就越高,单位面积内路网的数量就高;反之,城市交通网络越简单,城市交通网络的连通性就越低,单位面积内路网的数量就越低。 2.1.2 通达性模型 (1)距离可达性,即一个给定的节点到其他各节点最短距离之和。此距离越短,表示该节点的可达性越好。式(6)中
交通道路网的分枝维数反映交通网络的联通情况和空间结构的复杂性,如果分枝维数越高,说明城市交通网络越复杂,城市道路网的连通性就越高,单位面积内路网的数量就高;反之,城市交通网络越简单,城市交通网络的连通性就越低,单位面积内路网的数量就越低。 2.1.2 通达性模型 (1)距离可达性,即一个给定的节点到其他各节点最短距离之和。此距离越短,表示该节点的可达性越好。式(6)中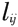 表示节点i到节点j的最短距离,则节点i的距离可达性定义为:
表示节点i到节点j的最短距离,则节点i的距离可达性定义为: