修订日期：2012-03 1 引言 随着传感器数量的不断增长以及遥感(RS)、地理信息系统(GIS)、全球定位系统(GPS)的广泛使用，地学研究邻域产生了大量的观测数据。这些数据不再局限于传统的静态空间中，而是逐渐向时间维扩展，形成了时间序列数据[1]。时间序列中蕴藏着不同的模式，而不同的模式反映了不同的序列成因。因此，针对序列模式进行聚类，将其分为不同的类别成为我们认识序列数据，进而理解序列形成本质的重要手段。由此看来，针对时间序列数据的聚类方法研究具有非常重要的意义。 与传统的点数据聚类方法相比，针对时间序列的聚类具有一定复杂性。首先，时间序列数据具有高维性，在这巨大的维数中往往只有一小部分维度是与表现对象变化特征的簇结构密切相关的，而其他不相关或者相关性很小的维度会产生大量的噪声，从而掩盖了真实的簇结构[2]。其次，由于维度较高，数据稀疏，维度之间也很可能会有相关性[3]，传统的相似性度量方法难以发现真实的结果[4]。第三，时间序列相似性的定义多种多样，基于观测值的相似性度量只能发现表面的变化，没有体现事物的内在机制。两条序列即使观测值相差很小，也不代表序列就很相似(图1a)；同样，观测值完全不同，两条序列也有可能在某方面具有相似之处(图1b)。 目前，一些学者提出了许多方法来解决不同类型的时间序列聚类问题。这些方法大致可分为两种：①对现有的静态数据聚类方法进行改进使其能处理时间序列数据；②将时间序列数据转换为静态数据的形式，然后直接用静态数据聚类方法来进行聚类[5]。按照这个思路，时间序列聚类方法可分为基于原始测度数据的时间序列聚类和基于特征的时间序列聚类。基于原始测度数据的时间序列聚类，直接根据原始数据定义相似度，如欧氏距离，相关系数，DTW距离等，然后进行聚类。Liao总结了用于时间序列聚类的各种相似性度量方法[5]；Díaz根据相似性度量的定义中是否需要估计模型参数，将时间序列聚类方法分为有参数的聚类方法和无参数的聚类方法[6]。这些方法在现实生活中都有广泛的应用。然而，采用基于原始测度数据的时间序列聚类方法，不可避免地要面对高维数据的问题；此外，基于原始数据仅能发现序列表面的相似性，没有触及序列本身的内在机制，聚类结果有很大的局限性。基于特征的时间序列聚类方法，先对原始数据进行降维，抽取表征其内在变化机制的特征作为相似性度量的基础，然后运用各种聚类方法对这些特征进行聚类，不仅减少了计算量，解决了时间序列高维数据问题，而且还可以处理有数据缺失、不等长或采样不均匀的时间序列；最重要的是，基于特征的时间序列可以根据不同的应用问题选取合适的特征，从而发现时间序列内在机制中不同方面的相似性。 本文根据时间序列的不同特征，系统综述了基于特征的时间序列聚类方法的研究进展。首先介绍了时间序列的定义，概念以及各类特征；然后对基于特征的时间序列聚类方法进行了分析和评述；最后讨论了现有方法的问题和挑战，并对未来时间序列聚类方法研究进行了展望。 2 时间序列数据及特征 时间序列也称为动态序列，由一组随时间变化的观测量组成。与传统静态数据不同，时间序列是一类复杂的数据对象，描述了事物变化过程。 2.1 时间序列类型 时间序列有很多种。根据数据类型不同，可以分为数值型时间序列和类别型时间序列；根据采样时间不同可以分为均匀采样时间序列和非均匀采样时间序列；根据观测值维度不同可以分为单维时间序列和多维时间序列；根据统计特征不同可以分为平稳型时间序列和非平稳型时间序列。不同的时间序列具有的特征也不同，本文主要针对数值型时间序列，如果没有特殊说明，下文中出现的“时间序列”均指数值型时间序列。 2.2 时间序列特征 通常时间序列具有多个特征，每个特征刻画了时间序列的一个方面。从对时间序列不同层次上的认知可将时间序列特征分为3种：形态特征、结构特征以及模型特征。这种分类体现了人们对时间序列认识逐步深化的过程。 2.2.1 形态特征 时间序列的形态特征主要指时间序列的形状变化特征，包括全局特征和局部特征。全局特征描述了时间序列的起伏变化，如上升、下降、头肩模式(图2)等；局部特征则表现为时间序列局部时间点上的异常观测值，如不连续点，极值点、突变点、转折点等。在时间序列最开始的研究中，人们通常是先将时间序列画出来，然后直观地通过观察来研究时间序列的起伏变化或异常点。这类反映时间序列整体变化或局部异常，可以直观看出的特征，称为时间序列的形态特征。基于形态特征的时间序列聚类，可以发现具有相同形状的时间序列簇，寻求时间序列的起伏变化规律。
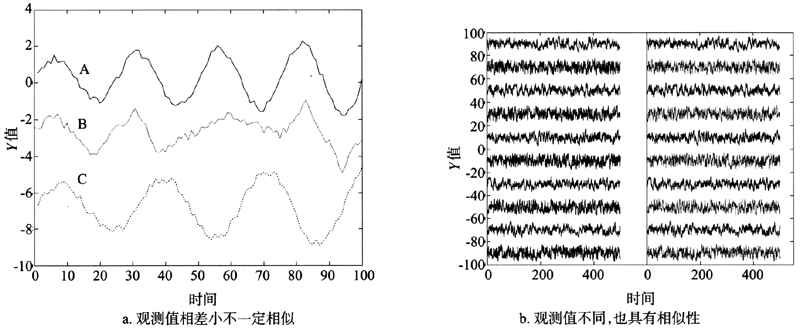
图1 观测值与相似性的关系 Fig.1 Relationship between observations and similarity of time series 注：a.A，B,C三条序列，计算基于标准化后观测值的欧氏距离，d(A，B)＜＜d(A，C)；但是直观上看，A和C两条序列显然更相似；b.序列的观测值之间难以看出关系，两两之间距离大体相等，但这些序列来自相同的创建机制：黑色序列来自系数为0.55，噪声方差为4的AR(1)模型，灰色序列来自系数为0.35，噪声方差为6的AR(1)模型。
