物流企业与贷款企业在存货质押融资中的演化博弈分析

      贷款企业将自有原材料、半成品或产成品作为质押物或担保物送至物流企业的融通仓，以获取所需资金的业务活动称之为存货质押融资。它弱化了企业担保及房地产抵押在借贷中的地位，从而大大缓解了中小企业融资难问题，对于合理引导流动性、解决当前流动性过剩的问题起到了十分重要的作用。由于我国存在社会信用机制不健全等问题，这种融资方式不可避免地存在信贷风险。因此，各主体融资时选择何种行为策略，哪些因素影响这些策略的选择，以及在既定策略下各方的收益多寡等都是理论界亟须研究的课题。根据文献检索，关于存货质押融资的研究大多集中在质押物的质押率[1-3]及折扣率[4-5]、贷款价值比[6-7]及贷款额度[8-9]、质押物的筛选[10]、物流企业选择[11-12]、物流企业与银行间的博弈分析[13]、质押信贷风险定价[14]、质押业务的影响因素[15-16]、风险评估及风险规避[17-20]等方面，目前针对上述问题，尚未有文献涉及。

      存货质押融资中的物流企业有两种参与方式。一种是作为银行和贷款企业的货物保管服务商参与其中；另一种是凭借银行授予的授信额度直接为贷款企业提供资金和质押物监管服务，即贷款企业向物流企业出质，物流企业将银行授予的授信额度分解给贷款企业，本文称之为授信融资模式。该模式较好地解决了我国商业银行无法混业经营的问题，在降低借贷门槛及提高贷款效率等方面均具有极大的优势，较之前者更具代表性。

      授信融资时，物流企业并不清楚贷款企业是否按合约规定使用资金，以及能否按时按量归还贷款。因此，有必要对贷款企业进行监管。据此，本文从物流企业和贷款企业仅具有有限理性的实际出发，借助演化博弈的方法，建立了贷款企业诚信和物流企业监管的演化博弈模型，进行了均衡点稳定性分析，得到博弈双方策略选择的决定因素以及演化稳定策略。最后，数值仿真了模型的演化轨迹，进一步验证了稳定性分析的结果。

      一、演化博弈模型

      融资合约生效后，贷款企业根据自身经营状况在资金使用及还本付息时存在两种行为选择：诚实和欺骗。物流企业对贷款企业也有两种行为选择：监管和不监管。由于物流企业与贷款企业的经营环境复杂多变，为便于分析，进行如下假设：一是博弈方为物流企业和贷款企业；二是贷款企业的策略选择为诚实和欺骗，物流企业的策略选择为监管和不监管；三是若贷款企业选择欺骗，物流企业只要监管就会发现其欺骗行为并进行相应的处罚。

      1.模型的构建

      根据上述分析和假设，物流企业和贷款企业的博弈收益矩阵如表1所示。

      

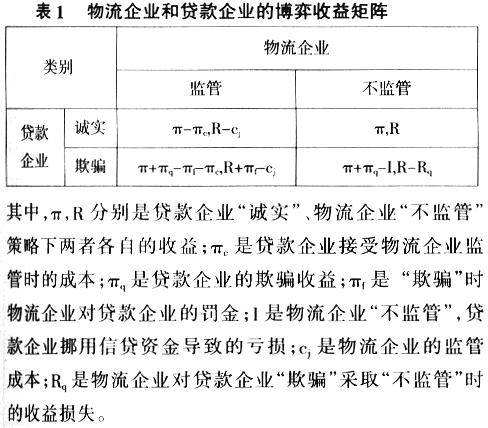      表1中的8个指标分别对应物流企业和贷款企业选择不同策略时的收益值，该收益矩阵能较好地反映物流企业和贷款企业在一次融资业务中的收益分配情况。若该博弈为一次性静态博弈，其纳什均衡为(诚实，不监管)。实践中，物流企业为保持稳定的客户群，贷款企业为保障获取贷款资金的便利性，他们的合作通常是长期且重复进行的。同时，由于信用体系不健全及博弈双方的有限理性，物流企业和贷款企业融资时受多种因素作用，要求根据对方的行为不断调整自身的策略，最终在试错中达到均衡。演化博弈论针对有限理性博弈方的策略和行为进行动态稳定性分析，由于具有较强的博弈论现实基础和高可信度的结论，因此，本文借助该理论研究物流企业和贷款企业策略选择的动态演化过程。

      2.复制动态方程和演化稳定策略

      博弈初始，假设贷款企业选择“诚实”策略的比例为x，选择“欺骗”策略的比例为1-x；物流企业选择“监管”和“不监管”的比例分别为y和1-y。由表1可知，贷款企业选择

      

      由式(5)，得到雅各比矩阵为

      

      将各均衡点的坐标值代入式(6)和式(7)，由J的行列式和迹的取值情况，分析局部稳定性如表2所示。其中，系统的不稳定点为(0，0)、(1，1)；鞍点为(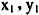)；ESS为(1，0)、(0，1)。

      物流企业和贷款企业的动态演化相位，见图1。其中鞍点E(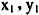)和2个不稳定均衡点(0，0)、(1，1)连成的折线可以认为是系统收敛于不同策略的临界线。当初值位于不同区域时，系统将收敛于不同的均衡点，说明初值对系统的演化结果有显著的影响；即初值位于折线上方区域Ⅰ时，系统将收敛于(0，1)点，其位于折线下方区域Ⅱ时，系统将收敛于(1，0)点。由表2可知，模型中欺骗收益、罚金和监管成本等参数同样影响系统的演化结果，这给贷款双方控制演化方向、制定经营策略提供了理论依据。