基于竞赛图法的区域科技创新能力评价研究

      0 引言

      科技创新能力是区域经济发展的基石，是区域经济发展的催化剂和助力器，更是全球化条件下决定区域参与国际产业化分工地位的关键性影响因素。科学的评价科技创新能力具有重要的理论与实践意义：一方面，有利于地方政府科学定位自身科技创新的处境，采取合理的科技创新战略，积极提升区域竞争优势，获取最佳的经济效益和社会效益；另一方面，有助于国家对于全国各区域的创新能力发展有一个科学的认识，通过分析找出宏观政策制定的缺陷，进而找到全国整体经济发展的方法和途径。

      从已有文献来看国内外学者主要运用[1-6]：模糊数学、SPA联系函数、因子分析方法、层次分析法(AHP)、神经网络(RBF)和主成分分析等方法对区域科技创新能力进行了研究。这里不再累述以上方法的具体研究情况与研究结论，通过分析我们认为已有研究主要存在的以下缺陷：第一，在指标体系选择及模型计算过程中存在人为因素的影响，这就降低了评价研究的结论客观性与可信度；第二，在选择指标体系时认为体系越大越能全面的反应评价问题的实际情况，然而却忽略了指标之间的信息重复性问题，这就会使得实证评价结果受到部分信息过分放大所带来的影响，从而丧失评价结论的客观真实性。由于以上问题的存在，各种研究方法的实证结论存在一定的差异性，我们认为必须寻找一种能够有效克服以上问题的方法，获得更加客观、真实、可靠的结论。本文从多属性决策视角入手，将区域科技创新能力评价过程看成是一个求解多属性决策问题，多属性决策问题——即有限方案多目标决策问题，其普遍存在于工程系统、社会经济、市场分析、管理等领域，是决策研究与方法研究的一个重要内容。本文应用离散数学中图论的方法对区域科技创新能力进行实证研究，同时为了避免以上问题的出现，首先，在指标体系的选择过程中，只选择具有统计数据的客观指标，以此来降低人为因素与主观因素的影响；其次，应用粗糙集法对指标进行全面的优化，避免指标信息重叠而带来部分信息过分扩大的问题；第三，在权重的确定过程中，我们采用熵权法，有效的避免了主观因素的影响。

      1 竞赛图法基本理论

      图论是离散数学中理论丰富且应用广泛的学科之一[7]，竞赛图是图论中研究成果最为丰富的一个分支，已经取得了丰硕的研究成果[8-20]。所谓竞赛图指的是：任意两个顶点之间都由一条有向边相连的图，有向边的方向表明了两顶点之间的优先关系——起始的顶点的优先次序在所指向的顶点之前，如图1、2所示。

      

      

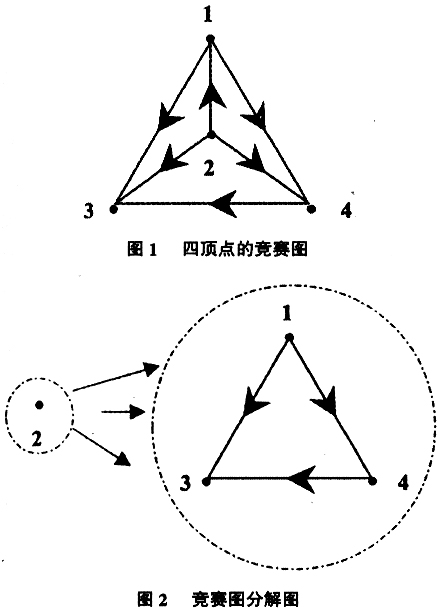
      2 竞赛图法的模型构建与实证研究

      竞赛图法是解决多属性决策问题的有效工具，本文首次将竞赛图法应用于处理综合评价研究方面的问题。将评价研究中表征区域科技创新能力不同方面的评价指标作为多属性决策问题中的各目标，并将指标的权重作为多属性决策问题各目标的权重。在此基础上，将待进行评价的各省市作为多属性决策问题待排序的方案，因此应用竞赛图法计算出的“方案”优劣排序，其实质就是各省市区域创新能力的强弱排序。

      2.1 竞赛图法的模型构建

      用竞赛图法来求解问题主要分为四步：第一，确定多属性问题的目标层；第二，计算出各目标层的相对权重值；第三，根据每个方案对各个目标的优先次序得出任意两个方案的优先关系；第四，根据两两优先关系，确定出竞赛图，并计算出方案的最终排序。竞赛图法的模型建立如下[21-24]：

      (1)确定“目标层”。

      多属性决策问题的目标即决策者选择最佳方案的依据，结合上文分析可知，本文中目标层的确定实质上就是确定表征待评价问题各方面特点的指标，即确定最佳省的依据。在确定待评价指标时，为了避免不同指标之间存在信息重叠问题，本文采用粗糙集法对各“目标”进行属性简约：首先，确定决策规则表。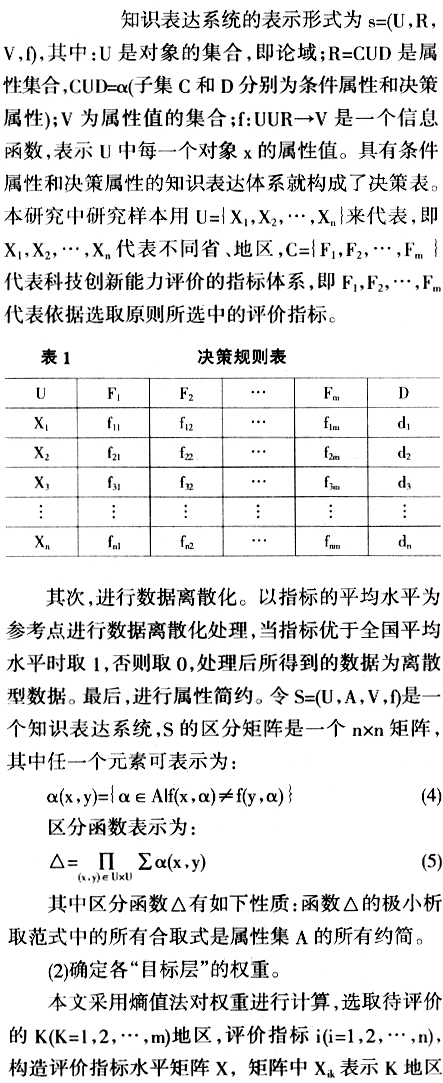

      

      

      

      

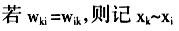      2.2 竞赛图法的实证研究