1 文献回顾 西方业绩评价起源于19世纪初，20世纪初期进入科学管理时期后，并得到长足发展。代表性的分析方法有沃尔业绩评价、综合评分法、杜邦财务分析法、EVA分析法等。 我国20世纪90年代才开始关注物流活动的评价，21世纪才付诸实践，对整个物流系统绩效评价方面的研究也逐渐增多，所建立的指标体系也日趋完善。在理论方面：周涛等利用模糊综合评判法对物流企业绩效进行综合评判[1]；胡晓燕提出了基于成本指数的物流评价体系[2]；何明祥、李冠等提出用数据包络分析法对物流绩效进行评价[3]；魏新军提出用模糊聚类方法来分析物流绩效[4]；曹坤提出利用主成分分析统计方法对物流企业绩效进行评价[5]；张滢提出基于熵权和灰关联的第三方物流企业绩效评价[6]。但以上的研究仅停留在理论上，并未进行实证分析。在实证方面：符想花对2003-2005年物流业上市公司的净资产收益率、总资产报酬率、总资产周转率、流动资产周转率、资产负债率、已获利息倍数、销售（营业）增长率、资本积累率8项指标进行了分析[7]；张宝友，黄祖庆运用数据包络分析(DEA)法，选取2002-2005年间的数据对我国深沪两市14家上市物流企业进行管理绩效评价[8]。但前者只是单纯地从各项指标出发缺乏综合性，后者采用的DEA法只就有效性做出评价缺乏具体性。因此在研究过程中本文将充分地考虑指标的综合性和具体性。 由于因子分析是统计中常用来直观和具体地综合反映出各因素对事物的影响的一种简便的方法[10]。本文将选用因子分析的方法对物流上市公司2006-2008年的经营业绩进行实证分析。 2 实证分析 2.1 数据来源及样本选择 本文选取上市物流公司近三年财务数据。然后针对已核实的上市公司样本，还需要根据以下条件进行过滤，从而使其符合实证分析的需要： 1)删去在三年研究窗口期间解体，或财务信息缺失及造假的企业； 2)排除在海外上市的中国企业。部分有实力的中国企业目前只在美国或香港上市，遵循国际会计准则制定财务报表，柳岸青、管亚梅研究发现国内与国际会计准则的若干差异必定会对上市公司报表产生深远影响，从而影响相关财务指标的衡量与计算[11]，因此为保证对财务指标考量的统一性与准确性，本文只能略去这些海外上市的企业，集中研究国内上市的物流企业。 因此通过以上的筛选，共获得样本公司24家。 2.2 指标体系的确立及样本数据的预处理 综合考虑评价指标的全面性，本文构建指标体系如表1所示。 根据确定的样本公司及建立的绩效评价体系，本文从上交所和深交所数据库中提取相应公司2006年、2007年及2008年年度财报中相应的财务数据。 接着本文使用SPSS14软件及Excel软件对样本数据进行预处理及进一步确定工作。包括： ①对财务数据按三年窗口期进行分类；②剔除数据中的特异值，作为缺失处理；③由于因子分析的前提是进行分析的原始指标间具有较强的相关性，因此须对指标体系分别进行三年窗口期的Kaiser-Meyer-Olkin及Bartlett球形检验，以确保因子分析能够顺利进行。经检验，若将所有评价体系中的指标都纳入因子分析范畴，在某些年份虽通过了Barlett球型检验，但KMO值略低于0.5，不利于因子分析的精确性(Kalse:1974)。因此依据对两年窗口期因子分析使用程度的检验，最后确定使用以下指标进行综合
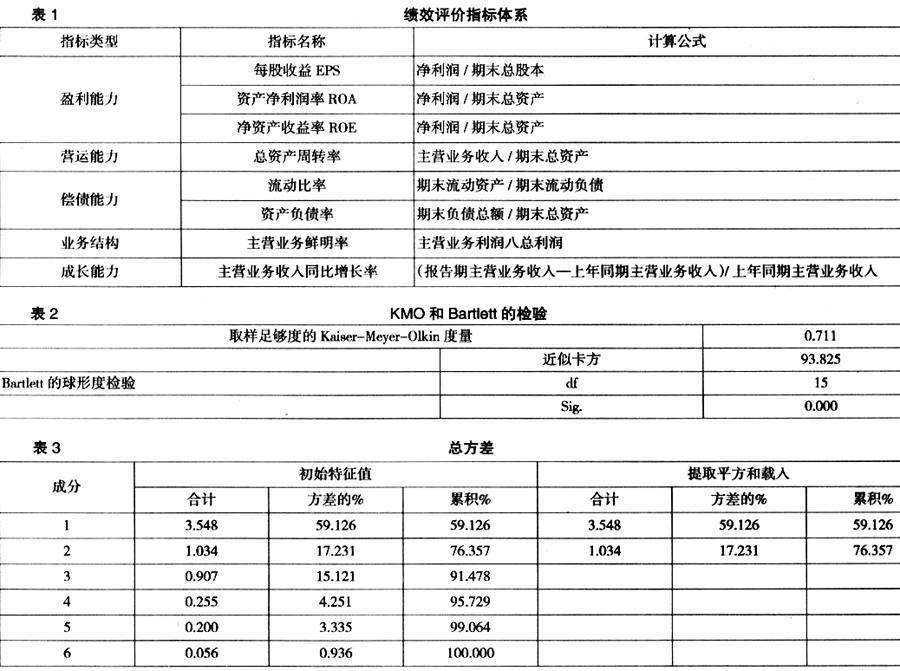
2.3 实证分析过程 本文将以2008年为例来叙述分析过程。 2.3.1 因子分析的可行性检验 对2008年的数据进行Kaiser-Meyer-Olkin及 Bartlett球形检验。检验结果如表2所示。 由表2可知：Bartlett球形检验的Sig值为0.000，非常显著，同时KMO的测度值为0.711，大于0.5以上，说明该指标体系适合进行因子分析(Kaiser1974)。经检验，其余二年的Bartlett球形检验的显著性水平均为0.000且KMO的测度值均在0.5以上，因此可以进行下一步的因子分析。 2.3.2 提取因子及因子载荷矩阵 下一步即为提取因子，综合考虑特征根及因子累计方差贡献率，本文选取2个因子并获得对应的因子载荷矩阵。以下为2008年的方差贡献率表和因子载荷矩阵，如表3、表4所示。= 从表3可以看出，前三个因子的累计方差贡献率为91.478%，能较好的反应原始数据的信息。
