供应链牛鞭效应的风险预测模型

      0 引言

      供应链系统中的牛鞭效应又称需求变异放大效应，是指供应链的需求信息从末端(客户端)向始端(原始生产端)传递时呈现波动程度逐级放大的现象。牛鞭效应的产生给供应链上下游的企业带来严重的损失，它不仅带给供应链上游企业错误的市场信息，使其难以得出合理的企业能力需求规划，错误的安排生产，加大库存投资，收益减少，并使整个供应链的运作成本过高，同时还会导致运作效率降低以及顾客满意率下降。

      学术界已经提出了不少预测分析理论，以期降低牛鞭效应的影响，提升供应链的运行效率。目前较为经典成熟的理论模型主要有自回归(AR)模型、系统动力学模型和Kalman 滤波器模型这三种方法。在简析这几个定量模型的基础上，本文提出了基于SVM的牛鞭效应风险分析预测模式。支持向量机(SVM)是在统计学习基础上发展起来的新一代学习算法，能很好地处理回归问题(时间序列分析)和模式识别问题，并已经被成功地推广到预测和综合评价领域。目前国际上SVM正处于飞速发展阶段，在文本分类、手写识别、图像分类、生物信息学等领域获得了较好的应用。本文将根据对牛鞭效应的形成有重要影响的五个指标进行分析，在一定假设前提下，建立牛鞭效应风险预测模型[2][3]。

      1 供应链牛鞭效应的风险因素分析

      供应链牛鞭效应首先来自于需求预测的不确定性，上游管理者总是将来自下游的需求信息作为自己预测的依据，并据此安排生产计划或供应计划。但是由于客观环境的复杂性和人们认识能力的局限性，使得顾客需求预测带有明显的不确定性，特别是革新性产品的需求预测。另外，各层节点企业为防止缺货，往往设定安全库存和订货点，而且订货的提前期越长，市场的波动越大，需求预测越不准确，“牛鞭效应”表现越明显。

      同样，风险也来自于限量供应下的短缺博弈，将有限的生产按照零售商所要求的订货量比例进行分配的方式，会导致牛鞭效应的放大，而在供应链中常会出现这种高需求的产品供给短缺的情形。设某供应商接到的总订货量为X，而其生产能力仅为x/2，则该供应商倾向于向每个分销商提供仅占其订货量一半的供货量，也正是由于在现实中许多制造商奉行这种分配方案，因此各分销商或零售商都用激励来放大自己的订货量。对潜在限量进行博弈的结果使上游企业不能从下游企业的订单中得到有关产品需求情况的真实信息，无法区分需求增长中有多少是由于市场的真正需求而增加的，有多少是零售商害怕限量而虚增的。

      提前期是在供应链的供需环节中下游顾客需要某种物品时，上游供应商需要提前准备该物品的时间。从牛鞭效应的数学表达式(1)可以看出，提前期对牛鞭效应的大小有直接的关系。提前期越长，则牛鞭效应越大。

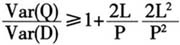      (1)

      其中L为提前期，P为预测样本数，Var(Q)为制造商收到的订货方差，Var(D)是零售商面对的需求方差。

      

      制造商和分销商常周期性地使用特殊促销方式，如价格折扣、数量折扣和特殊奖励等，这就引起了价格波动。在供应链中，这些特殊促销方式的运用在促进消费者大量购买的同时产生未来库存在这种模式下，可以预见，当商品价格低时，消费者所购买的比实际需要的要多，在商品价格回复到正常水平时，客户将减少或停止购买行为，直到库存耗尽。其结果是，消费者的购买模式无法反映实际的消费模式，并且购买数量的变化大于消费数量的变化，即引起了供应链中的牛鞭效应。

      供应链企业响应速度的快慢将会带来时间延迟问题的大小，又称时滞，时间延迟包括信息延迟和物流延迟。其中信息延迟主要来自于订单业务延迟、订货延返和邮寄延迟；而同样，由于制造商生产的产品需要经过批发商和零售商等中间环节才能交付到顾客手中，势必引起物流延迟，这又分为两种，交货延迟和运输延迟。

      2 基于SVM的供应链牛鞭效应风险预测模型

      2.1 风险预测模型分析

      支持向量机SVM(Support Vector Machine)是AT & Bell实验室的V.Vapnik提出的针对分类，预测和回归问题的统计学习理论。SVM的主要思想可以概括为两点：(1)它是针对线性可分情况进行分析，对于线性不可分的情况，通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分，从而使得高维特征空间采用线性算法对样本的非线性特征进行线性分析成为可能；(2)它基于结构风险最小化理论之上在特征空间中建构最优分割超平面，使得学习器得到全局最优化，并且在整个样本空间的期望风险以某个概率满足一定上界[4][5]。