空间关系推理方法分类体系

      中图分类号：P208 文献标识码：A 文章编号：1672—0504（2009）03—0001—07

      0 引言

      空间关系及其推理广泛用于空间数据查询[1]、空间数据挖掘[2]、基于内容的图像检索[3]、空间关系的等价性和相似性[4]以及空间数据库的一致性维护[5—7]等。在上述应用中，有关矢量对象或图像对象的知识用少量符号组成的空间关系描述，如inside、overlap、contain、north和south等。定性空间推理利用符号空间关系的常识性知识，自动从已知空间关系的符号描述中推导出新的空间关系信息。这种推理是在蕴涵的知识和规则的基础上经过符号运算而完成的，无需几何计算。空间关系推理在以下领域发挥作用：1）检查现实世界中是否存在一些空间对象，其空间关系可以满足查询语句或空间关系的符号描述，基于空间关系推理，可发现符号描述中与实际情况不相符的空间关系；2）检测多源、多尺度空间数据的不一致性，以维护空间数据的逻辑一致性；3）评价多源、多尺度空间数据的等价性或相似性；4）确定一个空间关系符号集能否充分且唯一地描述一个空间场景[6]；5）提高多种空间关系约束的空间数据查询或结构检索的效率。

      目前空间关系推理研究主要集中在单类型空间关系推理上，即根据拓扑关系推理拓扑关系、根据方向关系推理方向关系，而较少研究多种类型空间关系的混合推理。现有的各种空间关系描述模型相互独立，不能统一描述，因而较难进行多种空间关系的混合推理。空间关系推理是地理信息科学、人工智能、计算机科学等领域研究的热点，已提出了许多推理方法。为对这些推理方法进行分析和评价，需建立一套分类体系，并按照分类体系对已有方法的适用条件及解决的问题进行对比分析，了解各种方法的针对性和特殊性，不仅有利于正确理解和使用已有推理方法，更有助于研究和提出新的空间关系推理方法。但目前缺乏相关的分类体系，本文拟建立空间关系推理方法的分类体系，并在此体系内对已有方法进行对比分析。

      1 空间关系推理分类体系

      

      

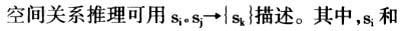
      在实际应用中，使用哪种空间关系推理取决于已知的空间信息及待推理的空间关系。Sharma进一步指出，集成空间关系推理所得结果与其它3种推理方法组合推理所得结果相同[8]。

      Sharma在上述分类的基础上，对方向关系采用投影模型，拓扑关系采用九交模型，定性距离采用间隔表示，实现了上述4种推理方法。由于用投影方法描述简单面对象的方向关系，因而不能正确推理方向关系；尤其是他仅关注简单方向关系推理，而没有涉及复杂方向关系推理，推理的效率和准确性受到限制。若用方向关系矩阵建模面对象的方向关系，推理结果会更精确，因此探讨方向关系矩阵和拓扑关系组合推理方法非常必要。

      1.2 基于空间关系描述模型的分类

      当采用不同的模型对同一对象的空间关系建模时，往往会有不同的结果。同样，采用不同的模型，也会导致不同的推理方法和结果。根据空间关系推理方法所采用的模型，可将空间关系推理分为基于同种模型及组合多种模型的推理。其中，基于同种模型的推理指已知和需要推理的空间关系均由相同的模型描述，包括基于RCC模型的拓扑关系推理[9]、基于九交模型的面对象拓扑推理[10]、基于投影方法的方向关系推理[11]、基于方向关系矩阵的方向关系推理[12]等。组合多种模型的推理指已知的空间关系采用不同的模型描述，需要推理的空间关系可为两个模型中的任一个，其典型例子为组合内部方向关系和外部方向关系推理内部或外部方向关系[13]、组合多种方向关系的拓扑关系推理[14,15]、组合九交模型和通用交模型推理线／面拓扑关系[16]等。

      需要指出的是，不是任意的两种模型组合都有意义，如组合RCC模型和九交模型没有意义，组合关系矩阵和锥形模型也没有意义。只有两个模型描述的空间关系概念不同，确实能提供互补信息时，组合才有意义。如方向关系矩阵和内部方向关系互补，因而可以组合推理；而方向关系矩阵和投影方法都描述外部方向关系，它们是竞争关系，因而其组合没有意义。

      1.3 基于参照系统的分类

      空间关系推理本质是一种符号运算，因而在运算中，须考虑符号的含义及其参照系统。这里的参照系主要针对方向关系而言，因为拓扑关系和距离关系没有参照系，但方向关系的定义和描述却离不开参照系。已有方向关系推理主要针对两个参照系，即两个已知方向关系的参照对象不相同：如从A与B及B与C间的方向关系推理A与C的方向关系或拓扑关系；在该例中，两个已知方向关系的参照对象分别是A和B。在实际应用中，由于已知方向关系和未知空间关系的条件限制，可能需要另一种推理机制：已知A与B及A与C间的方向关系，推理B与C的方向或拓扑关系；在这种推理中，两个方向关系共用1个参照对象A，因而为基于1个参照系的空间关系推理[14,15]。基于1个参照系的推理是对基于2个参照系推理方法的有益补充。