基于经济性和时效性的城市配送中心选址模型研究

      中图分类号：F253.9 文献标识码：A 文章编号：1003-1421(2009)02-0056-04

      在物流系统中，配送中心的选址往往决定着物流的配送距离和配送模式，进而对物流配送的时效性产生决定性的影响，因而研究配送中心的选址具有重要的意义。许多学者对此进行了深入研究。高自友研究了基于双层规划方法的物流中心选址问题[1]；姜大元应用Baumol-wolfe模型，对多物流节点的选址问题进行了研究[2]，该模型属于整数规划和非参数规划结合的模型；关志民等分析了影响配送中心选址的主要因素，并建立了相应评价指标体系，给出了一种定性和定量方法有机结合的模糊多指标评价方法[3]。这些模型和方法很好地解决了在物流节点选址过程中交通费用的计算、节点建设费用的计算和节点动态选址等问题[4]。上述研究主要考虑的是选址的经济性，而未考虑消费者对送货速度的要求，因此不能解决诸如救灾物资供应、易腐食品供应和军事后勤补给等时效性要求高的配送中心选址问题。为此，在综合考虑以上要求的基础上，以经济性要求为决策目标，以时效性要求为约束条件，建立配送中心选址模型，并借助LINGO 9.0寻求最优解。

      1 城市物流配送网络

      优秀的城市物流配送网络能够保证商品及时送达，加快商品流通速度，满足供应方和消费者的内在需求。配送网络设计是一个很复杂的问题，必须依靠科学的方法进行决策。总体要求是在多个消费者周边建立小型配送中心，保证一个片区的送货任务，充分发挥物流系统的网络优势。

      研究问题的描述：某城市有多个供应点供应数种商品，并经由配送中心送达消费者，每个消费者由某一指定配送中心独家供货。这些供应点的供应能力已知，消费者对每种商品的需求量已知，供应点和消费者的地理位置已知。要求从备选的配送中心中选择一个或多个配送中心，在满足消费者送货时间要求条件下，使整个配送系统的总体成本最小。这里的总体成本包括供应点商品的供应成本、供应点到配送中心的运输费用、配送中心的固定投资和管理费用、商品在配送中心的流通加工费用，以及配送中心到顾客的配送费用[5]。

      问题描述的配送系统可以看成一类二级运输系统，如图1所示。

      

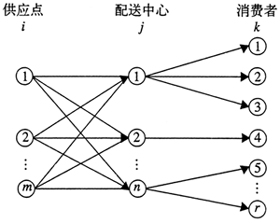      图1 城市物流系统配送网络

      2 配送中心选址优化模型

      2.1 建立模型的相关假设

      (1)仅在一定的备选地点范围内考虑新的配送中心设置。

      (2)每个消费者有且仅有一个配送中心为之配送货物。

      (3)不考虑运输成本的规模效应。

      (4)计划期内消费者对各类商品的需求量和供应点的供应量能够预测。

      (5)配送中心的可变成本为流量的凹函数[6]。

      (6)配送中心的容量和个数受到限制。

      2.2 模型的建立

      如果配送网络能够在一定时间内将商品送达消费者，说明消费者距网络中最近配送中心的距离不超过一定值。即可以将问题的时效性约束转换成配送中心到消费者的最大允许配送距离约束。

      在上述假设条件下，建立以下模型：

      

      

      公式(1)表示整个配送系统总成本最小，包括商品供应成本、运输成本、配送中心固定投资、配送中心变动成本及配送成本；公式(2)、公式(3)分别表示供求约束；公式(4)、公式(5)分别表示配送中心的容量限制及数量限制；公式(6)表示每个消费者的配送距离必须在允许范围内，以满足时效性要求；公式(7)表示未被选中的配送中心的流通量为0；公式(8)表示每个消费者有且只有一个配送中心进行商品配送；公式(9)表示消费者所需商品只能由其所属配送中心配送；公式⑽表示配送中心规模；公式(11)、公式(12)、公式(13)为决策变量。

      模型中的目标函数表示了选址问题的经济性要求，而将时效性要求等效转化成为最大配送距离的限制，用约束条件(6)表示。

      对于此类模型的求解，有许多启发式算法，如遗传算法等，在此利用LINGO 9.0求解。这是美国LINDO系统公司开发的专门用于求解最优化问题的软件包，可以十分方便地求解大规模线性规划、整数规划和非线性规划等问题。

      3 算例分析

      

      (1)问题1：不考虑时效性约束，确定配送中心选址结果。对于问题1，只需要将模型中的时效性约束，即约束条件(6)去掉即可。其对应的最优决策变量如表3所示。