基于灰色

      中图分类号：F270.7文献标识码：A文章编号：1002-3100(2008)10-0019-04

      1 问题的提出

      随着经济全球化、网络经济和电子商务的迅速发展，逆向物流已逐渐成为企业竞争的最前沿。为了获得竞争优势以及满足可持续发展的要求，企业必须将逆向物流纳入企业战略管理的高度上，提高企业的声誉和利润。

      然而相对于正向物流，逆向物流在数量、时间和质量等方面存在着高度的复杂性和不确定性[1]。这些不确定性的存在，对逆向物流的预测难度以及预测精确性提出了严峻的挑战。

      在灰色系统领域，GM(1，1)模型被广泛应用于不确定问题的预测，并且预测效果很好。在一些特定问题中，GM(1，1)仍然是决策者乐于选择的预测模型。传统的GM(1，1)模型主要是用于时间短、数据少、波动小、具有长期趋势的预测对象，对随机性波动较大的序列进行预测，其预测精度不理想，拟合度较差[2]。马尔柯夫预测是通过反映各种随机因素的影响程度以及各状态之间的转移的内在规律性来预测系统的未来发展方向[3]。适用于随机波动性较大的序列的预测，正好弥补了GM(1，1)模型预测的缺陷。

      综上所述，对逆向物流量的预测采取灰色预测和马尔柯夫预测两种方法结合，取长补短，用灰色预测模型来揭示长期发展的某种总趋势，而用马尔柯夫模型来确定状态之间的转移关系，建立灰色—马尔柯夫预测模型对逆向物流量进行预测具有重要的理论与现实意义。

      2 模型的建立

      2.1 灰色预测模型建立

      

      

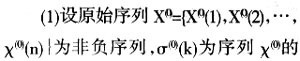
      对逆向物流而言，是基于反应的，它通常不是公司计划或决策的结果，而是对消费者行为或下游成员行为的反应，所以逆向物流量主要随时间而变化，呈现波浪式变化曲线，具有非稳定、波动大的特点[4]。这些波动性的存在，在运用GM(1，1)时可能产生病态性。所以必须根据原始序列的分布特点，通过级比检验，判定是否适合GM(1，1)建模。

      (3)数据变换

      对不符合惯性要求序列寻求合适的数据变换，保证处理后能够进行GM(1，1)建模。

      

      2.2 马尔柯夫预测模型建立

      马尔柯夫预测是根据初始的状态概率向量和状态概率矩阵来推测某一变量未来某一定时期所处状态的一种方法，其理论基础是马尔柯夫过程，其描述的是一个随机时间序列的动态变化过程。

      (1)状态划分

      根据马尔柯夫链将数据划分为多个不同的状态，用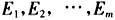来表示，一般通过实测值和预测值之间的相互关系进行状态划分，划分依据可以根据实际情况而定。例如文献[5]采取实测序列和预测序列的残差相对值序列的均值和方差的方法划分5个状态空间。文献[6]采用实测序列和预测序列的相对值进行划分，而在文献[7]人为将股票价格的波动划分为上升、持平、下降等三个状态。文献[8]运用上下边界线和上下极限线对序列划分为4个区间。

      (2)状态转移概率矩阵

      

      2.3 灰色—马尔柯夫预测模型的建立及求解步骤

      (1)灰色预测模型建立及求解

      根据2.1GM(1，1)模型建立及求解步骤，求解出预测曲线。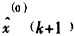

      (2)状态划分

      

      B——落入预测曲线以下的实测值与预测值相对值的均值

      C——实测值与预测值差值的最大值

      D——预测值与实测值差值的最大值

      (3)状态转移概率矩阵

      计算并确定状态转移概率矩阵。

      (4)编制预测表[5]

      选取离预测点最近的S个月份，按照预测时间的远近，转移步数分别定为1，2，…，S，在转移步数对应的转移矩阵中，取其初始状态所对应的行向量，从而组成新的概率矩阵，对新的概率矩阵将其向量求和，其和最大的转移步数所对应的状态即为系统的未来转向状态。