物流网络系统配送路线的优化方法

      建立在经济区域上的一个现代物流网络系统的物流节点可以是一个城市、一个产业集群，也可以是经济区域内某一个产品、商品的供应点。优化物流网络系统内工业生产的产业链的原料、半成品和产品的配送系统；农副产品加工基地的城镇居民供应链的鲜活农副产品的配送系统；旅游景区接送游客游览景点车辆的行驶路线都是人们非常关注的一个问题。它关系到能否为生产、商贸和居民消费提供快捷、准确、安全、高效优质的现代物流服务，降低系统物流成本和提高系统的经济效益，促进区域经济协调发展等。

      1 优化物流系统配送车行驶路线的动态规划模型

      我们可以根据物流网络系统所处的地理位置、交通运输条件、配送物资的供求关系等等客观因素将物流网络系统划分成若干个子配送系统。

      不妨分为T个子配送系统，t=1，2，…，T。

      问题：假定在一个时间周期内，从这个子系统的配送中心(节点1)发出一辆配送车到该系统内其它各个节点配送物资，经过每一个节点一次且仅一次，最后回到节点1，试问配送车应沿着什么路线行驶总距离最短？

      以下用动态规划的方法研究这个问题。

      建立物流系统配送车行驶路线的动态规划模型如下：

      

      状态变量用(i，Q)表示，即配送车从节点1出发，行驶到节点i，中间经过的节点的集合为Q；(i，θ)表示配送车从节点1出发，直接行驶到节点i，中间不经过其它节点，其中θ表示空集。

      决策变量表示决定配送车从节点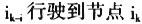

      

      

      最短路线上紧前的一个节点i[，k]。

      在优化每一个子配送系统的基础上，最后可以实现整个物流网络系统的配送最优化：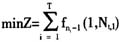

      

      其中Z表示T个子配送系统的配送费用总和，或配送车行驶的距离总和。

      2 实例分析

      例1：假如某一个城市的商品连锁公司下属五个商品超市，每天连锁公司从配送中心发出配送车将商品配送到每一个超市，表1给出配送中心和五个超市之间的距离(单位：公里)，要求配送车从配送中心出发经过每个超市一次且仅一次，最后回到配送中心，求配送车行驶的最优路线和最短距离。

      为叙述方便起见，把配送中心、超市1、…、超市5依次编号为节点1、2、…、6，由题设条件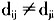，i≠j；i，j=1，2，…，6。此配送系统的交通图是一个有向多重连通图。根据上述讨论，我们采用顺推的方法求配送车行驶最优路线和最短距离：

      

      

      

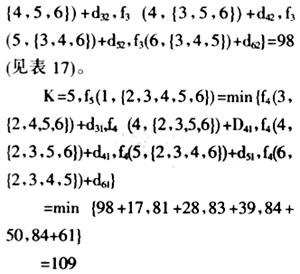
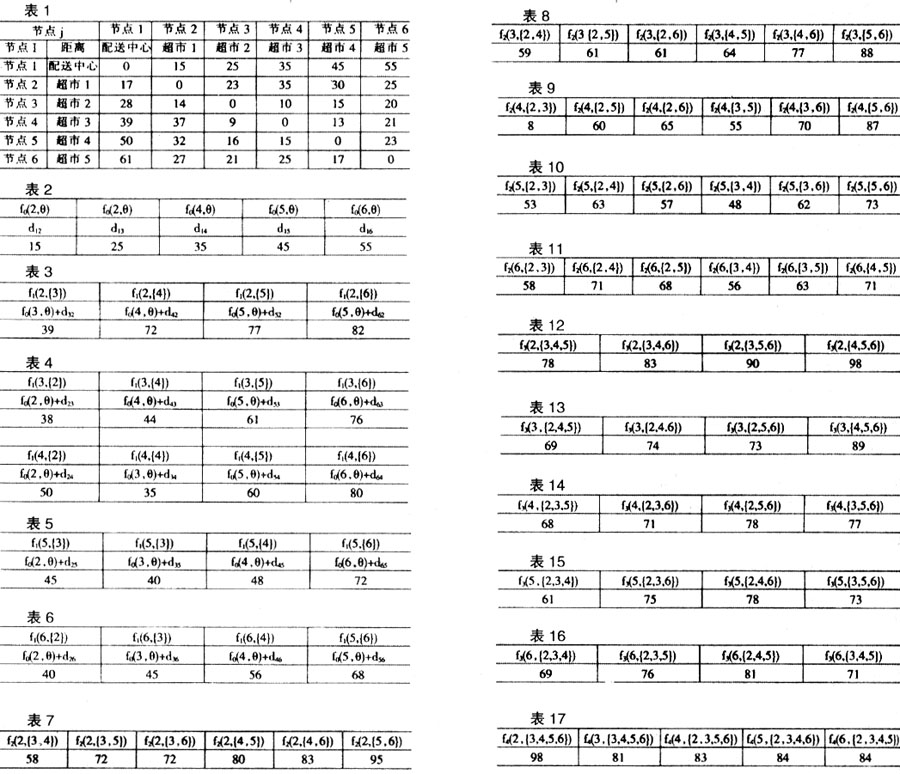      配送车最佳行驶路线：①→②→⑥→⑤→④→③→①，最短距离为109公里。

      从实例分析中可以看到，当物流配送系统的节点数n不大时用人工计算的方法比较容易求得最优解，当节点数较大时需借助相关的软件进行计算。

      3 优化物流系统配送车行驶路线的静态规划模型

      

      

      表示配送车从节点1出发经过每一个节点一次且一次再返回到节点1的一条行驶路线。

      当解向量X是问题的最优解时，它给出配送车从节点1出发经过每一个节点一次且一次再返回到节点1的一条最短的行驶路线。

      综上所述，物流配送车最优行驶路线问题可以在先不考虑条件(3)的情况下用解指派问题的匈牙利法求解。当所得的最优解满足条件(3)时，它就是物流配送车最优行驶路线问题的最优解，否则就不是。这种方法的计算量比用动态规划方法的计算量小得多。用动态规划的方法的计算量为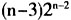，n是物流配送系统中节点的个数，随着节点个数的增加计算量越来越大。