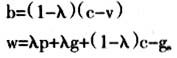一、引言 供应链协调与合作是供应链管理的核心问题之一。自上个世纪八十年代以来,该问题受到了工业界和学术界的广泛关注,提出许多使供应链合作的合约,如:回收合约[1]、收益共享合约[2]、数量折扣合约[3]、销售补偿合约[4] 等。Cachon[5]、Tsay等[6] 对这一方面的研究成果给出了全面的综述。供应链协调与合作至今仍然还是管理科学的一个研究热点。但是,以前的研究都是基于传统的库存管理模式,即,销售商从供应商处订货,订购的货物归销售商所有,未售完的货物所造成的损失由销售商负责,由于缺货而引起的缺货损失也由销售商负责,销售商基于自己的利润最大化选择订货量。由于需求的不确定性所引起的风险,销售商的订货量小于使供应链利润达到最大的订货量,这就导致双边际效应。为了鼓励销售商多订货,消除双边际效应,使供应链达到合作,或者供应商为销售商承担部分风险,或者供应商降低批发价,给销售商让利。因此,目前使供应链达到合作的合约是如何激励销售商选择合适的订货量。 由于传统的库存管理和订货模式会造成信息扭曲和牛鞭效应,这会给供应链管理带来更大的困难。为了克服这个困难,20个世纪90年代提出了供应商管理库存(VMI)的思想:即供应商直接面临市场,供应商根据市场的变化和仓库中的库存水平决定存货策略。仓库中的货物归供应商所有,销售商在销售商品时从仓库中取货。销售商只按实际销售量支付供应商款项,剩余没售完的商品,归供应商所有。因此,未售完的商品的贬值所造成的损失也是由供应商来承担。VMI最大的好处就是供应商能直接掌握市场的变化情况,准确预测需求,从而可以制定最优的存货策略。正因为如此,目前国内外许多著名的企业,如美的、联想、Dell、家乐福、沃尔玛等,都采用VMI。但是,我们看到,对于VMI来说,同样存在激励冲突。由于销售商要承担缺货损失以及由缺货而导致的商誉损失,销售商希望供应商多存货。但是供应商要承担未售完商品由于贬值而带来的损失,所以从供应商的利润最大化来说,供应商就会少存货。正是如此,与传统的库存管理一样,VMI同样存在双边际效应。为了使供应链达到合作,必须有一个机制保证供应商选择的存货量恰好是使供应链利润达到最大的存货量。 供应商管理库存环境下的供应链协调与合作引起了学界的广泛研究兴趣。在需求是确定的情况下,余玉刚等[7] 研究了VMI环境下的最优补货策略。Mishra和Raghunathan[8] 证明供应商管理库存会导致生产商竞争的加剧,从而使销售商获利。钟磊钢等[9] 提出一个使供应链合作的数量折扣合约。Bernstein,Chen和Federgruen[10] 在EOA(echelon operational autonomy)条件下,证明单一批发价能使供应链合作。在需求是随机的情况下,唐宏祥[11] 指出,零售商分担供应商的滞销风险和供应商承担零售商的部分促销费用能改善供应链的效率。曹武军等[12] 和蔡建湖等[13] 研究VMI环境下的收益共享合约,发现收益共享合约能提高供应链的效率。但是,到目前为至,在不确定需求情况下,我们还没有见到在VMI环境下使供应链合作的合约。本文提出了几个不确定需求,VMI环境下使供应链合作的合约。 本文的结构安排如下,第二节介绍基本模型,以及集中决策和分散决策所造成的决策不一致,即双边际效应;第三节提出几个使供应链达到合作的合约;第四节给出一些讨论和进一步研究的方向。 二、基本模型 本文研究由一个上游供应商和一个下游销售商(这里我们把下游称为销售商,而在实际生活中也可以是生产商)组成的一个二级供应链。考虑单周期问题,在周期初供应商决定库存水平Q。设这一周期的需求是随机的,为D>0。设F是需求D的累积分布函数,f是需求D的概率密度函数,则F是连续可微、单调增函数,且满足F(0)=0。 令

(二)分散决策情形 在分散决策情形,供应商和销售商是两个利益独立的主体。供应商决定库存水平Q,销售商只对实际销售商品支付每单位产品的批发价w,(c<w<p)。这时销售商的利润期望为

再由于F是增函数,得到Q*<Q。也就是说,存分散决策时,供应商的最优订货量小于使供应链达到合作的最优订货量,供应链不能合作。这说明在供应商管理库存环境下,同样存在双边际效应。必须有相应的机制激励供应商,才能使供应商的最优存货量恰是使供应链利润最大的存货量,供应链才能达到合作。 三、合作的合约 本节给出几个使供应链达到合作的合约。 (一)未售货物补偿合约 在这个合约规定下,销售商除了对已售商品支付批发价w外,还对供应商在仓库中未售产品支付一定的补偿b,以减少未售商品给供应商带来的损失,鼓励供应商多存货,这个原理与我们熟知的回收合约相似。在这个合约规定下,若供应商存货为Q,则供应商的期望收益为

即供应商的最优存货量恰是使供应链利润达到最大的存货量,供应链达到合作。由于λ∈(0,1)是任意的,这个合约能将供应链的利润在供应商和销售商之间任意分配。 由式(6)和式(7)可得
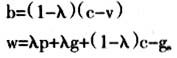
 (二)分散决策情形 在分散决策情形,供应商和销售商是两个利益独立的主体。供应商决定库存水平Q,销售商只对实际销售商品支付每单位产品的批发价w,(c<w<p)。这时销售商的利润期望为
(二)分散决策情形 在分散决策情形,供应商和销售商是两个利益独立的主体。供应商决定库存水平Q,销售商只对实际销售商品支付每单位产品的批发价w,(c<w<p)。这时销售商的利润期望为  再由于F是增函数,得到Q*<Q。也就是说,存分散决策时,供应商的最优订货量小于使供应链达到合作的最优订货量,供应链不能合作。这说明在供应商管理库存环境下,同样存在双边际效应。必须有相应的机制激励供应商,才能使供应商的最优存货量恰是使供应链利润最大的存货量,供应链才能达到合作。 三、合作的合约 本节给出几个使供应链达到合作的合约。 (一)未售货物补偿合约 在这个合约规定下,销售商除了对已售商品支付批发价w外,还对供应商在仓库中未售产品支付一定的补偿b,以减少未售商品给供应商带来的损失,鼓励供应商多存货,这个原理与我们熟知的回收合约相似。在这个合约规定下,若供应商存货为Q,则供应商的期望收益为
再由于F是增函数,得到Q*<Q。也就是说,存分散决策时,供应商的最优订货量小于使供应链达到合作的最优订货量,供应链不能合作。这说明在供应商管理库存环境下,同样存在双边际效应。必须有相应的机制激励供应商,才能使供应商的最优存货量恰是使供应链利润最大的存货量,供应链才能达到合作。 三、合作的合约 本节给出几个使供应链达到合作的合约。 (一)未售货物补偿合约 在这个合约规定下,销售商除了对已售商品支付批发价w外,还对供应商在仓库中未售产品支付一定的补偿b,以减少未售商品给供应商带来的损失,鼓励供应商多存货,这个原理与我们熟知的回收合约相似。在这个合约规定下,若供应商存货为Q,则供应商的期望收益为  即供应商的最优存货量恰是使供应链利润达到最大的存货量,供应链达到合作。由于λ∈(0,1)是任意的,这个合约能将供应链的利润在供应商和销售商之间任意分配。 由式(6)和式(7)可得
即供应商的最优存货量恰是使供应链利润达到最大的存货量,供应链达到合作。由于λ∈(0,1)是任意的,这个合约能将供应链的利润在供应商和销售商之间任意分配。 由式(6)和式(7)可得