宁波—舟山港一体化建设发展障碍与对策

      宁波港是浙江第一大港，具有经济实力、技术信息、经营管理等优势，但资源开发利用已近极限，需要谋求新的扩展空间；舟山港深水岸线资源丰富，但财力有限，加上身处海岛，直接经济腹地小，资金和技术力量不足，陆域的集疏运条件不完善，如要发展必须借助外力；宁波、舟山两港地理相邻，站在全局的角度，两港实施一体化建设是非常有益的。因此，专家建议，两港实行一体化建设。

      2003年，浙江省委、省政府作出推进宁波、舟山港口一体化决策部署。但是，从2003年到现在，宁波—舟山港港口一体化实际上仅停留在名义上，主要体现为两港原有名称“宁波港”和“舟山港”的撤销和“宁波—舟山港”新名称的挂牌，两港的管理未发生实质性变化。

      一、两港一体化建设发展障碍的博弈模型解释

      宁波、舟山港一体化建设进程几年来一直停留在名义上，表明存在发展障碍，我们试图建立动态博弈模型来予以解释，并且试图通过分析获得博弈均衡改变的激励机制。

      事实上，在宁波—舟山港一体化建设问题上，浙江省、宁波市、舟山市两级三地政府从实质上来说处于一种战略博弈状态：浙江省政府站在全省经济发展的角度，无疑是一体化建设的推动者，但由于宁波市计划单列市的身份，它必然同时要考虑合港后经济统计数据的归口的问题；宁波市政府基于宁波港口资源开发几近极限，而相邻的舟山港口优质资源大量闲置，为了拓展发展空间，无疑也是一体化建设的积极推动者，但也因为同样的原因而必然在谨慎观察；舟山市在这场博弈中，是最为弱小的一方，一方面由于经济发展的需要急于开发利用自有的优质港口资源以促进舟山经济的快速发展，另一方面又担心合港口之后资源被别人占有而丧失发展的本钱。三方在这场博弈中都在寻求最有利于自己的方案。

      因此，本博弈模型涉及三个参与人：第一是浙江省政府；第二是宁波市政府；第三是舟山市政府。

      假定浙江省政府的目标是在保证两个地区财政收入的基础上，使得两港的资源充分利用。浙江省政府有两个决策：加速推进一体化（以下用“一体化”表示）、维持现状（以下用“维持”表示）。宁波市政府和舟山市政府也有两个决策：积极参与一体化（以下用“积极参与”表示）、维持现状（以下用“维持”表示）。

      那么，我们用下面的方程表示浙江省政府的目标：

      

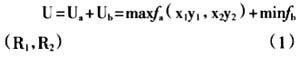      式中：U是浙江省政府的总效用；U[,a]表示两个地方政府的上缴的财政收入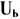；表示两个港口资源能够得到充分利用；表示两个港口闲置资源的函数；minf[,b]等价于maxLG（LG：两个港口资源充分利用后所产生的产值）。

      方程（1）可以转化为

      

      根据以上假设我们可以绘制出三个政府A（浙江省政府）、B（宁波市政府）、C（舟山市政府）参与博弈的博弈树（我们假设三个政府的决策顺序为A、B、C）：（图1）

      图1：三个政府参与博弈的博弈树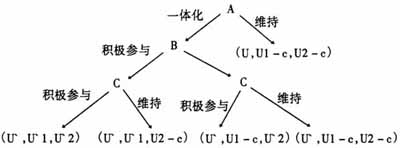

      

      这个动态博弈是否有均衡解，取决于支付函数的大小。如果B和C想选择不参与一体化进程，意味着B和C需要各自为自己的闲置资源寻找充分利用的机会，让A知道B、C的资源已经得到了充分的利用，即minf[,b]＝0，而这个过程需要花费成本c。我们考虑以下两种情况来试图分析这个动态博弈的均衡解。

      第一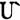，i＞Ui－c。首先A的最优决策一定是一体化（因为两港一体化以后，两港的资源互补，可以充分利用资源，所以l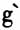＞lg）。从图1很容易看出C的最优决策是积极参与，给定C的最优决策，B的最优决策也是积极参与两港一体化。即此博弈的一个均衡解是（一体化、参与、参与）。我们对这个均衡的表述如下：如果一体化以后B和C的收益超过一体化之前的收益，那么B和C理所当然的选择积极参与两港一体化进程。