云南省图书馆机构用户,欢迎您!
地区综合实力反映一个地区社会经济系统的发展水平。主成分分析法能够在保证原始数据信息损失最小的情况下,以少数的综合变量取代原有的多维变量,使数据结构大为简化,并且客观地确定权数,避免了主观随意性,因而是地区综合实力评价的一种有效方法。通过主成分分析,可以全方位地了解各个地区社会经济系统的发展水平及其差距。
 (6)综合分析。一个m维主超平面究竟以多大的精度来近似代替原始变量系统,才能确保尽可能多的原始数据信息?这可以通过求累计贡献率
(6)综合分析。一个m维主超平面究竟以多大的精度来近似代替原始变量系统,才能确保尽可能多的原始数据信息?这可以通过求累计贡献率 来判断。一般取
来判断。一般取 大于80%的最小m(m<n),则可得主超平面的维数m,从而可对m个主成分进行综合分析。 2 地区综合实力的评价实例 地区综合实力反映了一个地区整体的经济实力和社会经济发展状况。因此,应该全方位地从一个地区社会经济系统的各个领域去选择指标。在第三届全国百强县的评选中,选择了22个指标:
大于80%的最小m(m<n),则可得主超平面的维数m,从而可对m个主成分进行综合分析。 2 地区综合实力的评价实例 地区综合实力反映了一个地区整体的经济实力和社会经济发展状况。因此,应该全方位地从一个地区社会经济系统的各个领域去选择指标。在第三届全国百强县的评选中,选择了22个指标: 前已述及,多指标的综合评价一方面增加了评价工作量,另一方面势必淡化主要指标的作用。为此,需要从现有指标中精选出若干个有代表性的指标。但人为地精选指标难免带有主观随意性,可能丢失部分有价值的原始信息。因此必须对所考虑的众多指标,利用数理统计法,经过正交化处理,使其成为少数几个相互独立的综合指标,再根据这些指标来评价一个地区的综合实力,而主成分分析法为实现这一思路提供了有效的数学方法[5-8]。本文以金华市社会经济系统的22个指标为例,来说明主成分分析法在地区综合实力评价中的应用。金华市位于浙江省的中部地区,共有9个县(市),分布在丘陵山地与河谷平原等不同的地貌单元内,社会经济系统的发展水平差异悬殊。
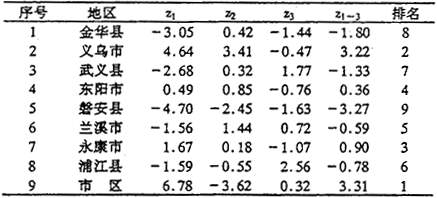
前已述及,多指标的综合评价一方面增加了评价工作量,另一方面势必淡化主要指标的作用。为此,需要从现有指标中精选出若干个有代表性的指标。但人为地精选指标难免带有主观随意性,可能丢失部分有价值的原始信息。因此必须对所考虑的众多指标,利用数理统计法,经过正交化处理,使其成为少数几个相互独立的综合指标,再根据这些指标来评价一个地区的综合实力,而主成分分析法为实现这一思路提供了有效的数学方法[5-8]。本文以金华市社会经济系统的22个指标为例,来说明主成分分析法在地区综合实力评价中的应用。金华市位于浙江省的中部地区,共有9个县(市),分布在丘陵山地与河谷平原等不同的地貌单元内,社会经济系统的发展水平差异悬殊。  表1 特征值、贡献率和累计贡献率 Table 1 Characteristic values,contribution rates and accumulative contribution rates 序号 特征值 贡献率(%) 累计贡献率 (%) 1 12.66 57.55 57.55 2 3.79 17.24 74.79 3 1.89 8.5783.36 4 1.52 6.9290.28 5 1.04 4.7395.01 6 0.53 2.3997.40 7 0.38 1.7199.11 8 0.20 0.89100.00 表2 各县(市)的主成分、综合主成分及其排名 Table 2 Every country's principal component,synthetic principal component and place
表1 特征值、贡献率和累计贡献率 Table 1 Characteristic values,contribution rates and accumulative contribution rates 序号 特征值 贡献率(%) 累计贡献率 (%) 1 12.66 57.55 57.55 2 3.79 17.24 74.79 3 1.89 8.5783.36 4 1.52 6.9290.28 5 1.04 4.7395.01 6 0.53 2.3997.40 7 0.38 1.7199.11 8 0.20 0.89100.00 表2 各县(市)的主成分、综合主成分及其排名 Table 2 Every country's principal component,synthetic principal component and place