上海大都市交通网络分形的时空特征演变研究

作 者：
刘妙龙/黄蓓佩 

作者简介：
刘妙龙(1944-)，男，上海市人，同济大学教授，博导，主要从事数量地理学、城市地理学与GIS研究。E-mail:longlm@sh163.net　同济大学测量与国土信息工程系，上海　200092 黄蓓佩　同济大学测量与国土信息工程系，上海　200092

原文出处：
地理科学

内容提要：

分形理论的城市形态发生学研究应用，首先是从交通网络的应用开始的。国内外学者进行的大量案例研究表明，分形分维有可能是表征城市交通网络特征、解释城市交通网络发展，演化的一种较为理想的测度指标。以上海这一国际性大都市的交通网络为研究主体，通过测算上海市不同行政区域交通网络的分维值，研究分形特征的空间变化；利用不同时代上海市全域及典型行政区交通网络的分维，研究分形特征的时间演化。研究结果表明，在上海与一些发展相当成熟的大、中城市与城市化地区，交通网络形态1.7左右的分形分维值具有普适性，有可能是判断网络形态与功能、结构完善度的一个较为合宜的测度指标；分维的变化，表现在空间域上，上海城市交通网络的分形特征内域明显复杂于外域，在城市发展主轴方向表现为由内向外分维测度值的有序降低；而在时间域，近期的交通网络分形复杂度明显高于早期，网络的构型不断得到优化；这一总体趋势，与城市形态开发、经济发展的历程相一致。可以相信，分形测度与分维的演化将成为描述城市形态发生学过程的一个最有用的指标。


期刊代号：K9
分类名称：地理
复印期号：2004 年 06 期

字号：大中小

      中图分类号：F294.3　 文献标识码：A　 文章编号：1000-0690(2004)02-0144-06

      1　城市交通网络分形的测度方法

      1.1　交通网络的分形特征与测度

      交通网络在一定的时间－空间域内具有明显的分形特征，已为大量的研究所证实。P.Frankhouser在1990年对德国斯图加特市郊区的铁路网络进行研究时[1,2]，发现了铁路网络长度L(r)与研究区域半径r之间的幂指数函数关系。一般地，设长度为L，面积为S，体积为V，则有：

      

      式中的r为区域半径，L(r)为半径为r的区域范围内的网络总长度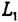，为常系数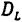，即为分维，Frankhouser将其命名为半径维数，以此测算的斯图加特市郊区铁路网络分形分维值为D≈1.58；国内刘继生[3]等利用相似方法测算豫南信阳地区公路网络的分维值D≈1.75。

      1.2　半径维数的地理意义

      半径维数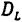反映了区域交通网络的分布密度由测算中心（一般是交通枢纽）向周边地区变化的动态特征[4,5]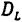，值越高，表明网络密度由测算中心向周边地区下降越慢乃至上升。对(4)式求导变换，可得交通网络密度的空间衰减表达式：

      

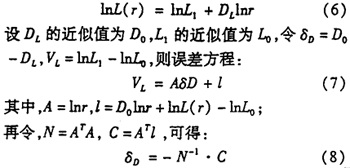      d=2即为欧氏维数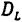，为半径维数。由密度空间衰减式可见：

      当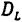＞2时，交通网络密度从测算中心向周边递减，交通网络强度尚未饱和，尤其在外缘地区尚有较大的发展空间；当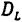=2时，交通网络密度从测算中心向周边变化均匀，交通网络强度饱和；当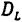＞2时，交通网络密度从测算中心向周边递增，若测算中心为网络交通枢纽，显然这种维数当属非正常维数。

      假定测算中心为交通枢纽，当测算得到的分维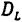值较高，且式(4)中的系数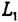较大时，意味着区域的通达性较好，交通网络的发育已较完善。

      1.3　半径维数的测算方法

      对(4)式作对数变换，可得

      

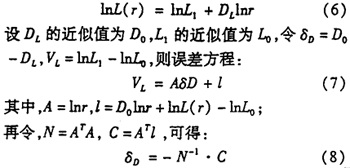      将(8)式代入(7)式和(6)式，可分别解得半径维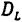数和常系数。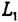

      如在研究区域内，以交通枢纽处为测算中心，选取半径r，量算该半径范围内即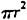面积中交通网络总长度L(r)；改变r，可得不同的L(r)，将点列[r,L(r)]标绘在双对数坐标图上，若点列呈对数线形分布，则该区域内交通网络密度具有分形特征表现，拟合直线的斜率即是交通网络的分维数。这种广为使用的分维数测算方法称为回转半径法。

相关文章：