GIS中矢量多边形网格化问题研究

      中图分类号：P208

      文献标识码：A

      文章编号：1672-0504(2004)01-0012-04

      地理信息系统(GIS)是对与地理空间相关的信息进行有效管理与综合分析的计算机系统，GIS把各种与空间信息相关的技术与学科有机的融合在一起，并与不同数据源的空间与非空间数据相结合，通过空间操作与模型分析，提供对规划、管理、决策有用的信息产品[1,2]。目前，GIS已成为处理空间信息的标准方法。CIS的核心功能是空间分析，它特有的对地理空间信息特别是隐含信息的提取、表现和传输功能[3]，是GIS区别于一般信息系统的主要功能特征。在进行CIS空间分析时，所获取的空间数据有相当大的一部分与一定的空间区域分布有关，对这些数据，多数GIS系统采用分层存储的方式进行处理，即将空间信息划分为众多专题图层（由于大多数区域单元的边界是不规则的，这些专题图层在数据结构上表现为不规则的矢量多边形），然后对这些专题图层进行相应的空间分析操作。但直接对这些不规则的矢量多边形区域进行各类空间分析操作并不容易，例如，区域叠加就是一类常见的空间分析操作，但由于矢量多边形的数据结构复杂，对矢量多边形区域进行叠加操作后常会出现“碎屑多边形”(Sliver polygon)，虽然可采用一些算法（如设定一模糊容限）来消除它，但这会明显降低空间分析的精度。另外，对多个矢量多边形区域叠加后的结果也不易进行其它分析与量算。因此，在进行实际的空间分析时，常常需要将边界不规则的矢量多边形区域转换为边界较为规则的格网状区域（如正方形、三角形或矩形区域），再对这些格网状区域进行各种空间分析操作与属性运算。相比于不规则的矢量多边形区域，格网区域的数据结构简单，易于在其上进行各种空间分析操作（特别是区域叠加操作），并可及时更新数据，从而使信息具有较强的现势性。本文介绍将不规则矢量多边形区域网格化为规则的格网区域时出现的问题及解决办法，在分析现有网格化算法的基础上，阐明各类算法的优缺点及应用领域，以期能对实际的GIS空间分析起一定的指导作用。

      1　矢量多边形网格化算法

      从本质上来讲，矢量多边形区域网格化是一个从源区域（不规则的矢量多边形区域）到目标区域（规则的格网区域）的转换过程，这种转换不仅包括区域边界形状的改变，更重要的是它还包括源区域所包含的属性信息到目标区域的属性信息的转换。按照属性信息转换规则的差异，矢量多边形网格化有四类算法[3-6]，即中心点归属法、面积占优法、重要性法和面积内插法。在矢量多边形网格化时，应使生成的格网区域尽量保持区域属性的真实性，最大限度保留或体现源区域所蕴含的属性信息。下面以一个简单的研究实例来说明各类算法的实现思想和应用范围。

      如图1所示，研究区域按照自然地理边界可划分为三个多边形区域A、B、C，各区的属性信息见表1。现在需要将研究区域网格化为50×50m的格网状区域（图2）。不可避免地，网格化后得到的格网区域可能有落在多个源区域的情况（如图2中含阴影斜线的格网区域a、b、c）。那么，究竟该按照怎样的规则才能实现最大限度地合理推定这些格网区域上的属性值呢？

      

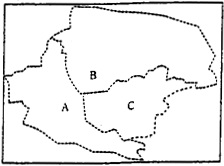      图1　源数据区域示意

      Fig.1 Sketch map of the source data zones

      

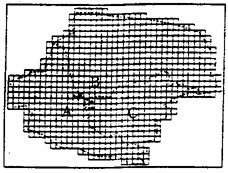      图2　网格化后的区域示意

      Fig.2 Sketch map of the gridding data zones

      表1　源数据区域属性信息

      Table 1 Attribute information of the source data zones

      区域

      面积()

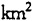      人口总数（人）

      人口密度（人／）

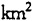      A　0.49

      13502755.1

      B　0.78

      15401974.4

      C　0.35

      10703057.1

      (1)中心点归属法是一种最为简单的属性判别方法，它将各个格网区域中心点所在的源区域的属性值作为整个格网区域（目标区域）的属性值。按照中心点归属法的规则，在图2中，网格a的中心点落在源区域B内，所以格网区域a的属性值与B同，即：面积为2500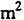，人口密度为1974.4人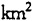／，人口总数为4.94人；网格b的中心点落在源区域C内，属性值与C同，即：面积为2500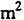，人口密度为3057.1人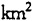／，人口总数为7.64人；网格c的中心点落在源区域A内，属性值与A同，即：面积为2500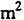，人口密度为2755.1人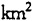／，人口总数为6.89人。一般而言，中心点归属法适用于具有连续分布特征的地理要素，如降水量分布、人口密度图等。在实际应用时，可能会有格网区域的中心点落在多个源区域的边界上而无法判别中心点位置归属的情况，这需要结合其他方法（如面积占优法、重要性法或者面积内插法）来确定，或者直接由分析者根据经验和需要来指定其属性值。