中图分类号 N092:/O112 文献标识码 A 文章编号 1000-0224(2004)03-0251-06 1 概述 《容圆七术》一书是清末数学家黄宗宪晚年的一部数学著作,是其著作集《古琴古砚斋算稿》中的一种,由梅城知足堂刊行于光绪二十二年(1896年)[1]。黄宗宪,字玉屏,湖南新化人,出生年代大约是19世纪40年代,同治十年(1871年)拜长沙丁取忠(1810-1877年)为师,从事数学研究[2]。在此期间,黄宗宪常与湘阴左潜(?-1874年)、湘乡曾纪鸿(1848-1877年)等人共同研讨数学问题,为《白芙堂算学丛书二十一种》的出版做了大量的校订工作,成为清末长沙以丁取忠为首的数学研究团体的重要成员之一[3]。光绪二年(1876年),黄宗宪随郭嵩焘一行出使英国,任供事,后又赴法国、西班牙等地,直到光绪八年春才回国[1,4]。黄宗宪的数学著作还有《求一术通解》、《曲面容方》、《悯笑不计》等[5]。 黄宗宪在《容圆七术》的序中说道:“山居日暇,检旧稿,有关制造测绘之用而为古法所未备者,摘录聚类而编之,颜曰容圆七术。”[6]从这段话中可以看到这样几层意思:其一,该书的主要内容在他作序时(1895年秋)之前很久就已经成稿;其二,他编写该书的主要目的在于应用;其三,他认为,书中应用于测绘方面的数学知识是前所未有的。 2 对《容圆七术》的分析及成果介绍 《容圆七术》分上、中、下三卷,上卷即给出了解决容圆问题的七术,共20道题。容圆问题是中国古代数学研究的古老课题之一,在这方面最具有代表性的著作是宋元著名数学家李冶(1192-1279年)的《测圆海镜》,该书给出170个问题,全都是围绕已知直角三角形求其内切圆、旁切圆及与之有关的线段而展开的[5]。《容圆七术》上卷在容圆问题上作了几步创造性的推广,即从直线三角形容圆到弧线三角形容圆的推广,从容一个圆到容多个圆的推广,从圆弧三角形容圆再到圆锥曲线弧三角形容圆的推广。《容圆七术》中卷又作了从相交的弧三角形容圆到相切、相离的弧三角形容圆的推广。 2.1 《容圆七术》上卷内容及成果 解决容圆问题的关键是根据已知条件求出所容圆的半径,《容圆七术》的上、中卷主要是采用代数方法求解,即每个问题都给出了以所求半径为未知数的代数方程,然后在细草中给出详细的推导过程。当然,上卷的第一术是个例外,因为它不仅给出了代数方程和推导过程,而且给出了几何解法,“以显数理之通”。下面就以第一术为例介绍其解法: “设如勾股容圆,有勾股及圆径各数,欲于三角各容递小诸圆,其术如何?术曰:以圆半径减股为小股,圆半径为小勾,求得小弦,以比例入之: 一率:圆半径加小弦(即图1中AF),
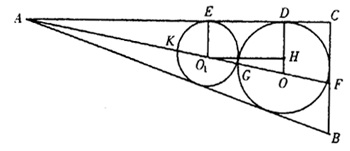
图1 三角容递小诸圆图 二率:圆半径减小弦(即图1中AG), 三率:圆半径(即图1中OD), 四率:递容圆半径(即图1中
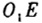
)。” 用现代数学符号来表示,即: 已知直角三角形的直角边AC及内切圆半径OD,求另一内切圆半径
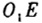
. 解:由勾股定理得
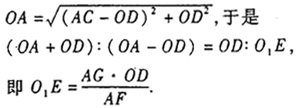
尽管西方数学早已传入中国,但是,黄宗宪在他的数学著作中仍然坚持使用中国传统数学的模式,即只给出算法程序,不叙述推导过程。当然,上述第一个等式成立是显而易见的,第二个等式的成立理由如下:
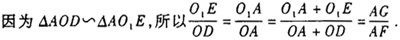
以上是黄宗宪给出的几何解法,下面介绍他的代数解法。 首先需要说明一点:《容圆七术》的所有代数解法中,未知数均以“天、地、人、物”等汉字表示,线段均以“甲、乙、丙、丁”等10个天干表示,图形上的点则以“子、丑、寅、卯”等12地支表示。本文对其代数解法的介绍,是用现代数学语言对其内容的一个直译:
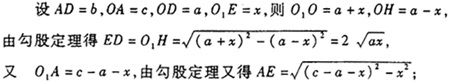
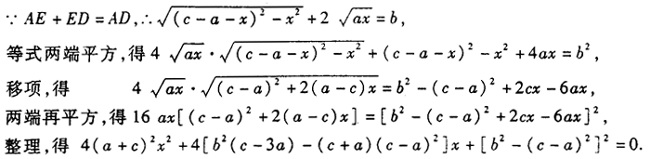
本文之后附有两个命题,以示推广:
 图1 三角容递小诸圆图 二率:圆半径减小弦(即图1中AG), 三率:圆半径(即图1中OD), 四率:递容圆半径(即图1中
图1 三角容递小诸圆图 二率:圆半径减小弦(即图1中AG), 三率:圆半径(即图1中OD), 四率:递容圆半径(即图1中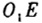 )。” 用现代数学符号来表示,即: 已知直角三角形的直角边AC及内切圆半径OD,求另一内切圆半径
)。” 用现代数学符号来表示,即: 已知直角三角形的直角边AC及内切圆半径OD,求另一内切圆半径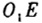 . 解:由勾股定理得
. 解:由勾股定理得 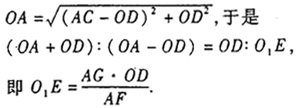 尽管西方数学早已传入中国,但是,黄宗宪在他的数学著作中仍然坚持使用中国传统数学的模式,即只给出算法程序,不叙述推导过程。当然,上述第一个等式成立是显而易见的,第二个等式的成立理由如下:
尽管西方数学早已传入中国,但是,黄宗宪在他的数学著作中仍然坚持使用中国传统数学的模式,即只给出算法程序,不叙述推导过程。当然,上述第一个等式成立是显而易见的,第二个等式的成立理由如下: 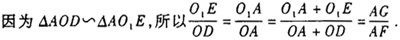 以上是黄宗宪给出的几何解法,下面介绍他的代数解法。 首先需要说明一点:《容圆七术》的所有代数解法中,未知数均以“天、地、人、物”等汉字表示,线段均以“甲、乙、丙、丁”等10个天干表示,图形上的点则以“子、丑、寅、卯”等12地支表示。本文对其代数解法的介绍,是用现代数学语言对其内容的一个直译:
以上是黄宗宪给出的几何解法,下面介绍他的代数解法。 首先需要说明一点:《容圆七术》的所有代数解法中,未知数均以“天、地、人、物”等汉字表示,线段均以“甲、乙、丙、丁”等10个天干表示,图形上的点则以“子、丑、寅、卯”等12地支表示。本文对其代数解法的介绍,是用现代数学语言对其内容的一个直译: 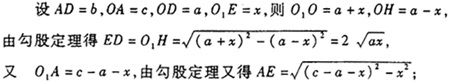
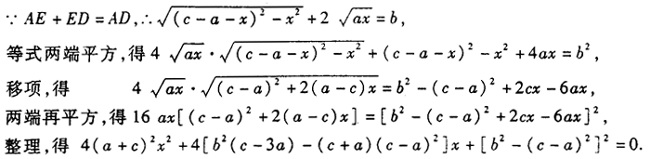 本文之后附有两个命题,以示推广:
本文之后附有两个命题,以示推广: