云南省图书馆机构用户，欢迎您！
研究表明，现有关于区域可达性的计算公式，其实质都是给定区域中某一质点的居中性的测量，因此，现有的区域可达性其实仅指区内可达性。据此，将区域可达性理解成由区内可达性和区外可达性2部分组成，并重点讨论了区外可达性的测算方法。研究表明，区外可达性定量模型的建立无法简单地套用现有的区内可达性的测算方法，原因是门户质点的区外可达性值由于距离为0故无法运用现有的公式予以测算，为此我们通过区外虚拟质点的引入巧妙地解决了这一难题。依据重新定义的区域可达性，本文在均质平原背景的假设条件下推导出了区域双核结构模式的形成机制及相应的参数条件。流域作为双核结构模式形成的理想区域，也在此得到了验证。由于区域双核结构模式仅是区域空间结构类型的一种，因此，随着模型参数的改变，即可进一步推导出其它的空间结构类型。这样，本文建立的关于区域可达性的系列测算公式，显然已不仅仅适合于区域双核结构模式的验证，而是一个适用于区域空间结构演化与区域空间结构类型分析的具有普适意义的数学工具。
应该说，还有其他很多相关的区域可达性测算公式，所用名称也各不相同，如位势、区位潜能、城市中心性、区域中心性[8-13]，等等。但所有基于空间引力模型基础上的区域可达性测算公式均大同小异，其实仅是区内可达性的测算。依据这样的计算公式，往往是越靠近所研究区域中心，则值越大，位于区域边缘的值则相对要小得多。因此，这样的区域可达性可称之为区域中心性，亦即是对所研究区域内各点的中心性的一种度量。 然而，对于区域内任意一点而言，其区位价值的评判并不仅仅由区域中心性来度量，还取决于与区外交往的便捷度。换言之，对于给定的区域而言，其区内任意一点的区位价值的评判应当是区内（区域中心性）和区外（对外便捷性）这2个部分的综合评判。为统一起见，我们将现有的区域可达性称为区内可达性，对外便捷性称为区外可达性，两者合称区域可达性。 1.2 区外可达性的测算依据与公式构建 不失其一般性，设：(1)区域内任意一点P[,i]的质量相同；(2)对外联系的方向仅有1个方向；(3)对外交流的货物都通过位于区域边缘的P[,0]点，以下称之为门户质点或门户城市；(4)区域A内任意质点P[,i]至门户质点P[,0]的距离为d[,i0]（图1a）。 对区内任意质点P[,i]而言，其与区外的联系可分为2种类型，一种是通过门户质点P[,0]中转，另一种是由质点P[,i]直达目的地而不在门户质点P[,0]中转。本文仅考虑前一种类型。这样，区内任意质点P[,i]的区外可达性的差异，就仅仅表现为该质点与门户质点P[,0]的联系便捷程度的差异。据此，参照区内可达性的计算思路与方法，设m[,i]、m[,o]分别为任意质点P[,i]和门户质点P[,0]的质量，则质点P[,i]的区外可达性R[,aoi]的计算公式可表述为： R[,aoi]=(m[,i]+m[,o])/2d[,io](2) 公式(2)似乎解决了区外可达性的定量测算问题，然而，深入分析后发现，区外可达性的测算远比现有的区内可达性的测算要复杂得多。原因在于，对于给定区域中的任意1个质点P[,i]，都可以计算出其区外可达性，唯门户质点P[,0]由于距离为0而不可能从公式(2)中求出结果。当然，更不能随意给门户质点P[,0]赋值，不然就失去了公式计算和结果推导的严谨性。 显然，如何科学地解决门户质点P[,0]的区外可达性的定量测算，就成为区外可达性甚至区域可达性系列公式构建中的关键难题。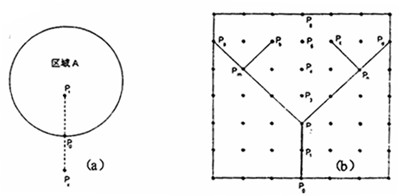 
图1 圆形均质背景(a)和k=7×7=49个质点的方形均质背景(b)下区外可达性计算示意图 Fig.1 Diagram to calculate accessibility under the homogeneous background of circle(a)and square(49 points)(b) 我们注意到，在给定的区域A中，区外可达性的最大值肯定分布于门户质点P[,0]（图1a）。这就为我们进行相应的计算提供了思路上的启发：我们虽然不能给出门户质点P[,0]的准确值，但是我们可以确立在门户质点P[,0]的区外可达性值为1时，区内各质点P[,i]的区外可达性的相对值（归一化值）。为此，在图1a中给定区域外A引入1个虚拟质点P[,x]，该质点也可理解为区内各质点P[,i]货物输送的目的地。由此即可构建定量测算区外可达性的系列公式：
