河口、陆架和海洋模式在胶州湾的应用

      中图分类号：X143

      文献标识码：A

      文章编号：1007-6336(2000)04-0013-05

      数值模拟与预测以其经济有效且可预测性的优点得到日益广泛应用。在海洋环境问题日趋严重的今天，要正确模拟那些具有不同比重而存在于不同深度的物质在河口、海湾中的迁移运输过程，则需要对流场进行三维模拟研究。目前沿岸浅海区三维潮流数值模拟方法研究仍较少。本文将普林斯顿大学的河口、陆架和海洋模式（Ecom模型）[1]，成功应用于胶州湾及扩大域，重现了胶州湾M[,2]分潮的时空分布，探讨其流场垂向变化规律。

      1　模型介绍

      本模型在垂向采用σ坐标变换、水平向采用曲线正交坐标变换，较好地拟合了近岸复杂的岸形和底形；采用湍封闭模式[2,3]更客观地提供垂向混合系数，避免其人为选取造成的误差；空间交错网格的采用和显式隐式结合求解，抑制计算误差短波的传播，具有良好的稳定性；在计算上采用分裂算子法求解，灵活、简单、经济、稳定且精度好。

      

      1.3　有限差分分裂算子法求解步骤

      将原来比较复杂的动量方程求解分解成三个简单问题的连续求解过程。具体方法如下：

      将[n·△t,(n+1)△t]分成三个时间过程，在前1/3时间步长由对流和扩散项，显式求解U[n+1/3,1]，U[n+1/3,2]。在2/3时间步长由垂向梯度项，隐式求解U[n+2/3,1]，U[n+2/3,2]。在后1/3时间步长将动量方程的水位梯度项和深度积分后的连续方程联立，U[n+1,1]，U[n+1,2]由水位η[n+1]表示，代入深度积分后的连续方程，得到η[n+1]的五点隐式格式，超松驰迭代法求出η[n+1]，从而进一步反代求得U[n+1,1]，U[n+1,2]。再由连续方程反求出真正η[n+1]和总水深D[n+1]及每一层的ω[n+1，k]。更新流速、水位、水深后，由显式隐式结合的方式（垂项梯度项隐式求解）求解湍能(q[2],q[2]l)方程，从而进一步求同扩散系数K[,M]、K[,H]、K[,q]、A[,M]。循环迭代计算。

      2　胶州湾潮流场模拟的应用

      2.1　计算条件

      模拟胶州湾M[,2]分潮潮流场。取计算域为灵山岛—沙子口弧线所围的海域。计算网格（图1）采用水平正交曲线网格自动生成技术[5]，考虑了胶州湾沿岸水域复杂的地形岸形和北部较大的潮间带，其空间网格0.4～1.5km；时间步长为186.3s；在垂直方向自海面到海底等分为五层；水界为：ζ(t)=H[,M[,2]]cos(σ[,M[,2]]t-g[,M[,2]])。取第五个潮周期计算结果分析。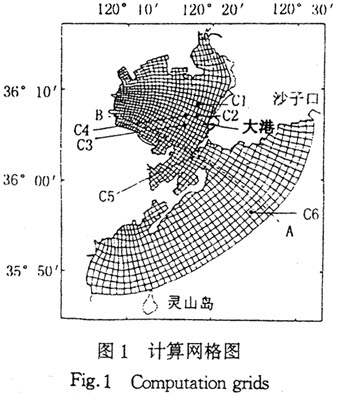

      

      2.2　计算结果验证

      M[,2]分潮同潮时线和等振幅线（图2）表明：在湾外潮波由东北向西南传播，属于反时针潮波系统。沙子口处发生高产灵山岛超前26min，海湾底部滞后湾口约8min；沙子口振幅不到115cm，随着潮波向湾内传播，振幅逐渐加大，到湾底部接近130cm。以上规律与1958年海洋普查的历史资料一致。

      

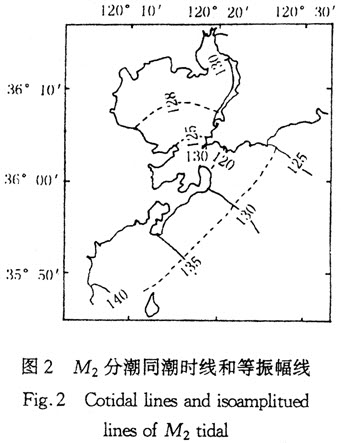      取大港潮位验证（图3），潮位振幅最大误差为1.15cm，位相最大误差6.3min；C1～C6六个站位的M[,2]分潮潮流玫瑰图验证表明其表层计算值与实测值的主流向、最大流速发生时、潮流旋转方向基本一致。

      上述验证结果表明，计算与实测符合良好。

      2.3　计算结果分析

      分析涨潮中间时水位和流场分布（图4），可以看出：涨潮中间时，沙子口水位-3.5cm，团岛为-20cm，湾底为-25cm，灵山岛为-35.5cm，潮流从东北涨入，部分沿岸朝西南流去，部分进入胶州湾，湾内为涨流，流速均很大，湾外为转流期。落潮中间时流场特征与涨潮相同，只是水位高低分布和流向相反，沙子口水位为3.4cm，团岛为20cm，湾底为26cm，灵山岛为35.2cm。涨、落潮最大流速均在胶州湾口，流速约为100cm/s。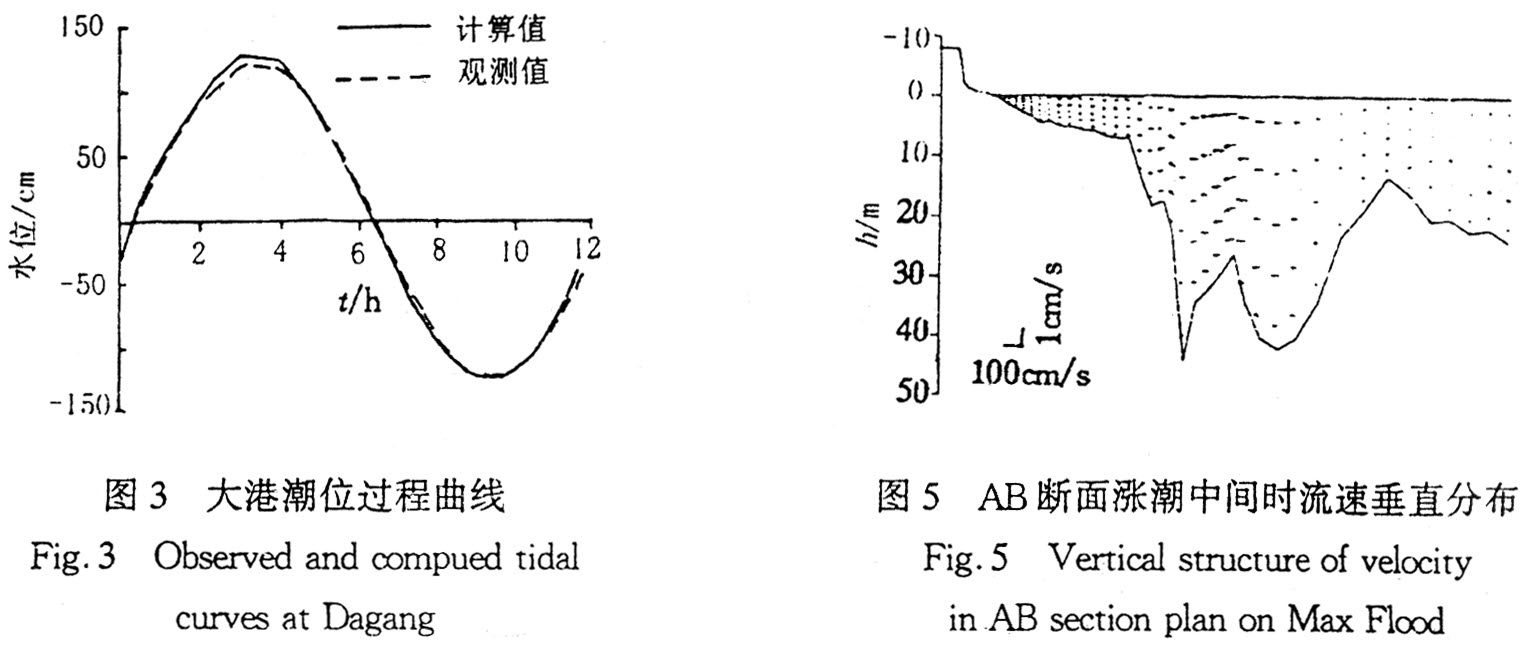

      

      

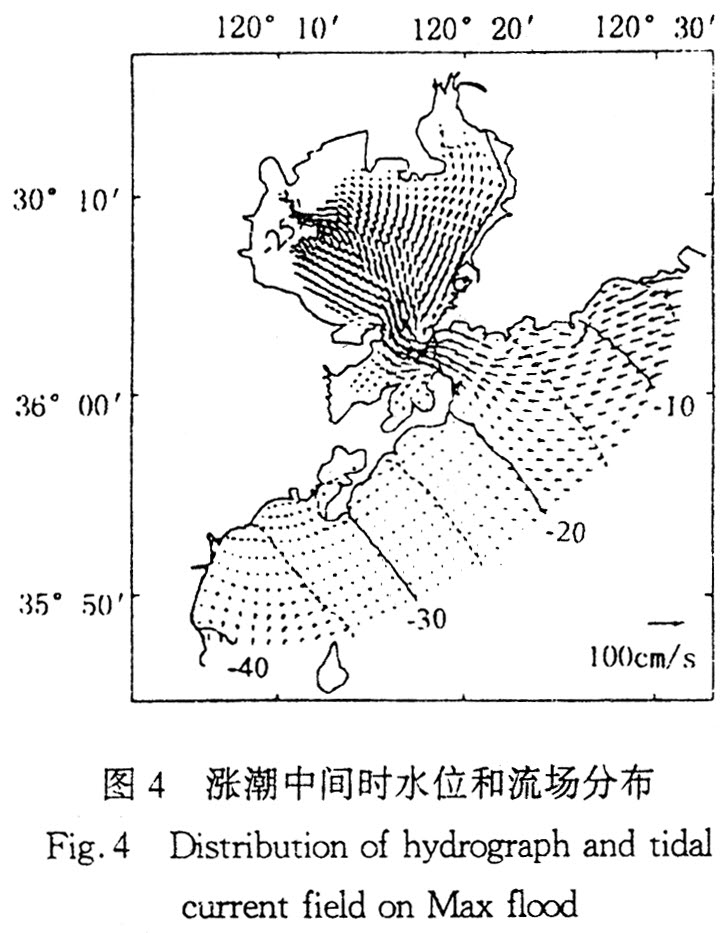      分析跨湾外、湾口和湾底的AB断面涨潮中间时刻流速生向分布（图5）可知：垂向流速较小，为10[-4]m/s量级；最大水平流速在湾口附近，最大垂向流速位于湾口略西北处海域底部，为30×10[-4]m/s；从表层到底层，水平流速逐渐衰减，垂向流速却逐渐增大。这是由于在密度均匀、无风状态下，在湾口略西北处海底地形起伏较大，潮流大幅爬坡或落降，从而产生较大垂向速度。落潮中间时与涨潮中间时流速垂向分布基本相似，不同的是流速方向相反。