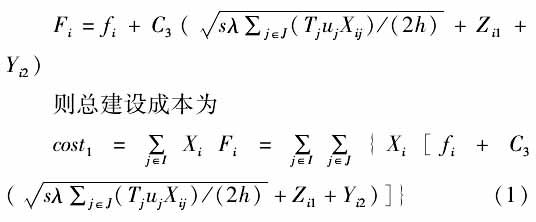文章编号:1005-2542(2019)01-0201-06 关于库存—选址联合优化问题,学者们基于配送中心级和需求级分别存储本级安全库存的假设取得了丰富的研究成果。少数学者对这种安全库存本级配置模式的科学性进行了进一步探讨,文献[1]中假设配送中心不存放任何库存,订货一到立刻根据分配策略配送给各个零售商。文献[2]中针对一个制造商、多个分销中心和多个零售商组成的多级配送系统,考虑零售商随机需求和相关需求两种情况,分别构建配送中心持有及不持有库存的多级库存系统成本优化模型。文献[3]中探讨多级配送系统中库存配置与需求量均值、方差的关系,发现需求量小时库存适合存储在配送中心层,需求量大时存储层向靠近客户的方向移动。文献[4]中分析了安全库存全部聚集在配送中心级或全部分散在需求级的利弊,提出每个零售商应根据其与配送中心的距离及其销售商品的需求量确定合适的安全库存配置策略,即差异聚集策略;并在考虑库存持有成本、紧急配送成本的基础上构建安全库存优化配置模型。文献[5]中考虑不同产品的需求不同,通过构建模型探讨了需要建立多少个配送中心、配送中心选址在何处、不同产品的安全库存应该存储在配送中心还是工厂等问题。上述研究均假设系统安全库存全部存储在配送中心级或需求级,未考虑以下部分跨级存储的情况:配送中心级的安全库存一部分存放在本级、另一部分存放在需求级;需求级的安全库存也可以同样决策。 配送中心建设成本与其容量大小紧密相关,若假设配送中心容量无限制,既不符合现实情况,也不能准确反映其建设成本。已有学者对配送中心容量有限制问题进行了如下研究: (1)配送中心容量固定。文献[6]中假设配送中心的容量受到限制、需求为在线需求、各个配送中心间存在库存共享,探讨了共享效应和运输成本之间的关系。文献[7]中基于(Q,R)策略,考虑容量有能力限制、需求服从正态分布,将库存策略与配送中心选址作为整体进行研究。 (2)不同容量水平对决策的影响。文献[8]中假设需求服从正态分布,给出不同容量水平下的建设费用,以建设成本、运输成本、经营性库存和安全库存成本最低建立模型。文献[9]中探讨需求一定,计划期、订货周期固定情况下的库存表达式,并给出库存费用和运输费用的权重,最后对容量因素作了敏感性分析。 (3)配送中心容量随需求变动。文献[10]中在需求半径和需求点的分布已知的前提下,假设配送中心容量是与市场需求相关变动的弹性变量,以利润最大或成本最低构建选址模型。文献[11]中假设以最大需求作为配送中心容量限额,各配送中心集中存放安全库存,构建了选址-库存模型。文献[12]中假设配送中心建设成本可变,且为配送中心规模的线性函数,构建指定备选点和不指定备选点的非线性0-1整数规划模型。但是安全库存量的大小也会影响配送中心的容量;而安全库存的配置模式又决定了安全库存量的大小。 关于部分跨级存储问题还未有相关文献,各级的安全库存应该如何配置、最优的部分跨级存储比例如何确定、安全库存配置模式对配送中心容量的影响等方面的定量研究是亟待解决的问题。 1 模型构建 1.1 情景假设 (1)单一产品、单周期、单一供应商、多配送中心、多需求点,供应商和需求点的位置已知。 (2)一个配送中心可以向多个需求点供货,但是一个需求点只能由一个配送中心进行配送。 (3)(Q,R)库存检查策略,给定备选地址,无容量约束。 (4)各需求点的需求完全独立且均服从正态分布。 (5)配送中心级和需求级分散存储安全库存,不存在横向转运和紧急调运的情况。 1.2 模型参数与决策变量 模型参数 I——备选配送中心集合,某一个配送中心用i表示 J——需求点集合,某一个需求点为j N——选定配送中心个数 K——用来衡量库存可得性指标,即库存安全系数,与服务水平有关

决策变量
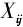
——0,1变量,如果需求点j由配送中心i服务,则取1,否则取0
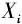
——0,1变量,如果配送中心选在i位置,则取1,否则取0 1.3 各项成本估算 (1)配送中心建设成本。配送中心建设成本考虑与其建设容量有关,配送中心i的标准差

配送中心i的建设成本=固定建设成本+变动建设成本其中, 变动建设成本=单位建设成本×(周转库存+安全库存)所以,配送中心i的建设成本为
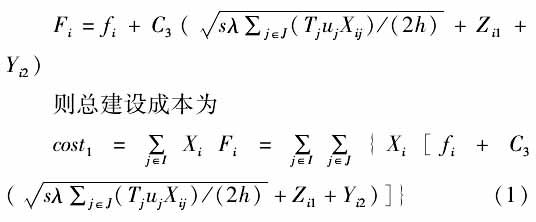
 决策变量
决策变量 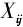 ——0,1变量,如果需求点j由配送中心i服务,则取1,否则取0
——0,1变量,如果需求点j由配送中心i服务,则取1,否则取0 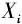 ——0,1变量,如果配送中心选在i位置,则取1,否则取0 1.3 各项成本估算 (1)配送中心建设成本。配送中心建设成本考虑与其建设容量有关,配送中心i的标准差
——0,1变量,如果配送中心选在i位置,则取1,否则取0 1.3 各项成本估算 (1)配送中心建设成本。配送中心建设成本考虑与其建设容量有关,配送中心i的标准差  配送中心i的建设成本=固定建设成本+变动建设成本其中, 变动建设成本=单位建设成本×(周转库存+安全库存)所以,配送中心i的建设成本为
配送中心i的建设成本=固定建设成本+变动建设成本其中, 变动建设成本=单位建设成本×(周转库存+安全库存)所以,配送中心i的建设成本为