一、引言 供应链管理环境下,库存管理的重要性越发显著。集成供应策略(I/S,Integrated Supply)于20世纪90年代初在维护、维修和操作(MRO)中出现,并得到迅速发展。在最常见的集成供应形式中,通过一个供应集成者(顾客的唯一接触者)来发展一个供应集团并负责给顾客提供所有的供应,其它供应商不能直接将货物运送给顾客[1]。I/S的最大优势在于资源分配的优化,由于各合作企业都独立工作于其核心能力,从而使得供应链管理水平得到提高。Ghodsypour[2]、Kim[3]、程海芳[4]、贺政纲等[5]等都对集成供应的相关问题进行过研究。 集成供应的一个重要问题在于,核心企业没有直接和供应商发生业务关系,失去了对供应商的直接控制。显然,对于企业重要的原材料或者零部件,企业并不愿意失去和供应商的联系。而第三方物流企业的发展使得集成供应模式得到了改进。第三方物流集成供应可以实现多批次配送的运输,从而减少因庞大的库存而引起的损失。第三方物流集成供应需要解决的关键问题在于集成供应成本如何在各供应商之间进行分摊,Aksoy等[6]对于集成供应的成本分摊问题进行过相应的研究,而博弈理论也在水资源开发和电力建设等领域的成本分摊中得到过应用[6]。本文将运用合作博弈理论中的夏普利值法来进行第三方物流集成供应成本的分摊,并引入风险调整以及经济订货批量模型改进了夏普利值法应用中的实际问题。 二、基于第三方物流的集成供应模式 传统的集成供应使得核心企业和供应商之间不直接发生业务关系,从而失去了对供应商的直接控制,在一定程度上也加大了核心企业所承担的风险。因此,在更多情况下,集成供应是被运用在企业备品备件或者辅助材料的采购管理之中。第三方物流企业的成功运作为集成供应模式在企业的应用创造了条件。按照“商流与物流分离”的原则,第三方物流企业只从事供应过程中的相关物流活动,而不参与相关的商流活动,从而使得集成供应的很多物流优势得到充分的发挥,另一方面,企业也不失去对供应商的控制。 在供应链管理中,在核心企业(制造商或零售商)越来越重视JIT供应的情况下,各供应商往往要屈服于核心企业的谈判能力,而在核心企业周围设立库存,以保证对其的JIT配送供应。这种模式在核心企业实现零库存的情况下,大幅增加了供应商的成本,从整个供应链的角度来说,并不一定是最优的。事实上,供应商成本的增加总会以某种形式转嫁给核心企业。 基于第三方物流的多供应商条件下的集成供应模式就是在这种情况下降低供应链总成本的一种有效方式。对于处在同一地区的供应商,由一个集成供应商(一般是一个第三方物流企业)制订全部物流计划,按照供需双方的供求信息,负责将货物从各供应商到用户的运输、储存和管理,以满足用户(制造商或零售商)的需求。图1描述了从各供应商自行供货模式到传统集成供应商供应模式,再到第三方物流集成供应模式的转变。 第三方物流的集成供应问题在很多情况下都适用,主要表现在:(1)大型制造企业的零部件采购与供应;(2)大型连锁商业企业的大规模采购供应;(3)行业采购联盟的采购供应等。
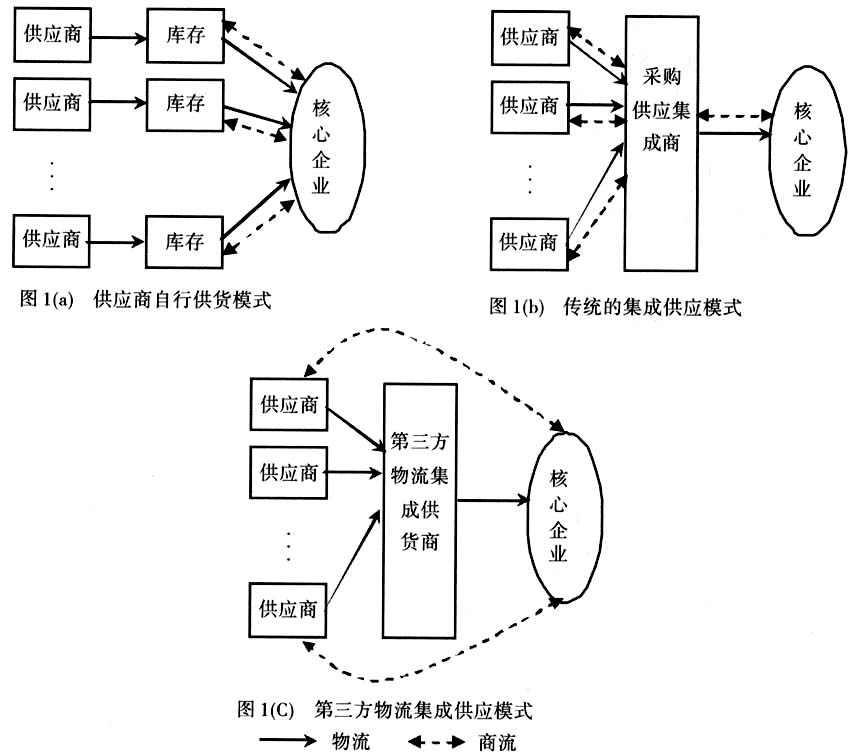
图1 从供应商自行供货到第三方物流集成供应 三、夏普利值法在集成供应成本分摊中的应用 集成供应成员企业之间是一种典型的合作竞争关系,集成供应成本如何在成员企业之间进行合理的分摊,是集成供应成本管理所要考虑的一个关键问题。 (一)夏普利值法的应用 夏普利值是1953年由Shapley L.S.给出的一个的概念,它不仅可以解决合作联盟中效益或成本分配的问题,而且能够估计社会活动中各团体或者派别的权利[13]。 Shapley认为,在特征函数满足超可加性的情况下,假设<N,C>为一个联盟博弈,对于给定的特征函数可以确定出特定的分摊向量

,应满足几条公理: (1)对称性公理。每个局中人i所得的收益(或分摊的成本)与i的序号无关。 (2)有效性公理。
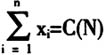
,有效性公理反映了
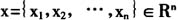
作为分摊的整体合理性。

 图1 从供应商自行供货到第三方物流集成供应 三、夏普利值法在集成供应成本分摊中的应用 集成供应成员企业之间是一种典型的合作竞争关系,集成供应成本如何在成员企业之间进行合理的分摊,是集成供应成本管理所要考虑的一个关键问题。 (一)夏普利值法的应用 夏普利值是1953年由Shapley L.S.给出的一个的概念,它不仅可以解决合作联盟中效益或成本分配的问题,而且能够估计社会活动中各团体或者派别的权利[13]。 Shapley认为,在特征函数满足超可加性的情况下,假设<N,C>为一个联盟博弈,对于给定的特征函数可以确定出特定的分摊向量
图1 从供应商自行供货到第三方物流集成供应 三、夏普利值法在集成供应成本分摊中的应用 集成供应成员企业之间是一种典型的合作竞争关系,集成供应成本如何在成员企业之间进行合理的分摊,是集成供应成本管理所要考虑的一个关键问题。 (一)夏普利值法的应用 夏普利值是1953年由Shapley L.S.给出的一个的概念,它不仅可以解决合作联盟中效益或成本分配的问题,而且能够估计社会活动中各团体或者派别的权利[13]。 Shapley认为,在特征函数满足超可加性的情况下,假设<N,C>为一个联盟博弈,对于给定的特征函数可以确定出特定的分摊向量 ,应满足几条公理: (1)对称性公理。每个局中人i所得的收益(或分摊的成本)与i的序号无关。 (2)有效性公理。
,应满足几条公理: (1)对称性公理。每个局中人i所得的收益(或分摊的成本)与i的序号无关。 (2)有效性公理。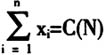 ,有效性公理反映了
,有效性公理反映了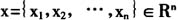 作为分摊的整体合理性。
作为分摊的整体合理性。 